
����Ŀ���������ʵء���С����ͬ��С��ֱ��������2����1��3�����һ�������Ŀڴ����ȣ���������һ��С��������![]() �Żؿڴ��н��ȣ�����������һ��С���ּ�������b�������͵õ�һ���������
�Żؿڴ��н��ȣ�����������һ��С���ּ�������b�������͵õ�һ���������![]() ��
��
��1���������![]() ǡ���ں���
ǡ���ں���![]() ��ͼ���ϵĸ��ʣ�(����������״ͼ�������б����ȷ��������������̣���������)
��ͼ���ϵĸ��ʣ�(����������״ͼ�������б����ȷ��������������̣���������)
��2����������ڴ�������![]() ����������2��С����ͬ���IJ������̣����õ��ĵ�
����������2��С����ͬ���IJ������̣����õ��ĵ�![]() ǡ���ں���
ǡ���ں���![]() ��ͼ���ϵĸ�����_________(���ú�
��ͼ���ϵĸ�����_________(���ú�![]() �Ĵ���ʽֱ��д�����)��
�Ĵ���ʽֱ��д�����)��
���𰸡���1��![]() ����2��
����2�� ��
��
��������
(1)�������⻭����״ͼ�����б������ݸ��ʹ�ʽ���㼴�ɵõ��𰸣�
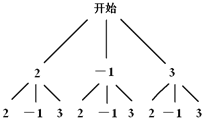
��2���������ڴ�������n��n��1������������2��С����![]() �ֵȿ��ܵĽ�������з���Ҫ��Ľ����2��n+1���֣�ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
�ֵȿ��ܵĽ�������з���Ҫ��Ľ����2��n+1���֣�ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��1����������õ���
��
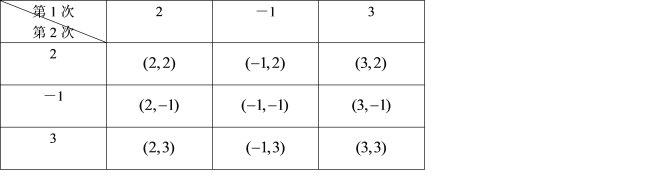
���9�ֵȿ��ܵĽ�������з���Ҫ��Ľ����2�֣�
��![]() (��
(��![]() ��)
��)![]()
��2���������ڴ�������n��n��1������������2��С����![]() �ֵȿ��ܵĽ�������з���Ҫ��Ľ����2��n+1���֣�
�ֵȿ��ܵĽ�������з���Ҫ��Ľ����2��n+1���֣�
�ʴ�Ϊ��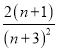 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A����1��0�����������꣨1��n������y��Ľ����ڣ�0��3������0��4��֮�䣨�����˵㣩�������н��ۣ���abc��0����3a+b��0���۩�
��x�ύ�ڵ�A����1��0�����������꣨1��n������y��Ľ����ڣ�0��3������0��4��֮�䣨�����˵㣩�������н��ۣ���abc��0����3a+b��0���۩�![]() ��a����1����a+b��am2+bm��mΪ����ʵ��������һԪ���η���
��a����1����a+b��am2+bm��mΪ����ʵ��������һԪ���η���![]() ����������ȵ�ʵ������������ȷ���У�������
����������ȵ�ʵ������������ȷ���У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016ɽ��ʡ�����У���ͼ��OΪ����ԭ�㣬�ı���OACB�����Σ�OB��x����������ϣ�sin��AOB=![]() ������������
������������![]() �ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F������AOF��������ڣ�������
�ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F������AOF��������ڣ�������

A. 60B. 80C. 30D. 40
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ��
��![]() ��
��![]() �dz�����
�dz�����![]() ��������A��
��������A��![]() ��
��![]() ���͵�B ��
���͵�B ��![]() ��
��![]() �����������ߵĶԳ�����
�����������ߵĶԳ�����![]() ������. ���н��ۣ� ��
������. ���н��ۣ� �� ![]() �� �� ����
�� �� ����![]() ���������ȵ�ʵ������ ��
���������ȵ�ʵ������ ��![]() . ���У���ȷ���۵ĸ����ǣ� ��.
. ���У���ȷ���۵ĸ����ǣ� ��.
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
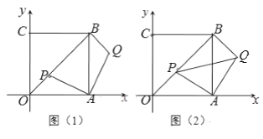
����Ŀ��ƽ��ֱ������ϵ�У��ı���OABC�������Σ���A��C ���������ϣ���B��![]() ��
��![]() ����P������OB��һ�㣬��
����P������OB��һ�㣬��![]() �Ƶ�A˳ʱ����ת90�㣬��
�Ƶ�A˳ʱ����ת90�㣬��![]() ��Q�ǵ�P��ת��Ķ�Ӧ��.
��Q�ǵ�P��ת��Ķ�Ӧ��.
��1����ͼ��1����OP = ![]() ʱ�����Q�����ꣻ
ʱ�����Q�����ꣻ
��2����ͼ��2�������P��![]() ��
��![]() ����
����![]() ����
����![]() �����ΪS. ��S��
�����ΪS. ��S��![]() �ĺ�����ϵʽ����д����Sȡ��Сֵʱ����P�����ꣻ
�ĺ�����ϵʽ����д����Sȡ��Сֵʱ����P�����ꣻ
��3����BP+BQ = ![]() ʱ�����Q�����ֱ꣨��д��������ɣ�
ʱ�����Q�����ֱ꣨��д��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ��С����ƵĴ�����ͼ���Ļ�����Ʒ������Ʒ������ͼ2��ʾ�ľ���ͼ��ƴ�Ӷ���(���ص�����϶)��С������ͼ��2�����жԳ�֮������������Գ�ͼ�Σ�Ҳ�����ĶԳ�ͼ�Σ��������ͼ�ν���̽����

��1����ͼ3����֪ͼ����һ���֣����������ͼ2��ͼ3��ͼ����������(Ҫ�߹���ͼ��������ͼ�ۼ�����д����)��

��2����ͼ4��![]() ��
��![]() ���ϡ���������Ӱ���ֵ����֮��Ϊ
���ϡ���������Ӱ���ֵ����֮��Ϊ![]() �����ڲ����������������ȵ�ƽ���������ཻ�õ���������ε��ܳ���
�����ڲ����������������ȵ�ƽ���������ཻ�õ���������ε��ܳ���
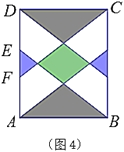
��3��С����Ϊ��ͼ4�е�4���հײ�����һ����������ƴ��һ��������(���ص�����϶)���������С��д��Ӧ���������(��ʾ�����![]() ��
��![]() �ij���֮�ȣ���ָ����
�ij���֮�ȣ���ָ����![]() ��
��![]() ���)��
���)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����������
��ͼ�٣���Rt��BAC�У���BAC��90������D��E�ֱ���CB��AB���е㣬��F��BD���е㣬��AB��8��AC��6����EF���� ����
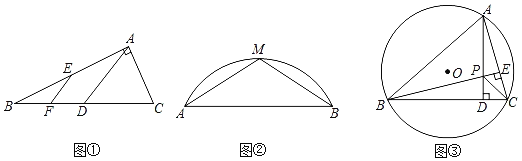
��2������̽����
��ͼ�ڣ���֪��M�ǹ���AB�ϵ��е㣬AB��24������AB�ĸ���8�����Ӧ��O�����Ϊ���٣�������������Ż�����
��3����������
��ͼ�ۣ��ڰ뾶Ϊ5�ġ�O�У���BC��8����AΪ�Ż�BC�ϵĶ��㣬����A��AD��BC�ڵ�D������B��BE��AC�ڵ�E��AD��BE���ڵ�P������PC��������PBC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
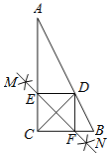
����Ŀ����ͼ��Rt��ABC�У���ACB=90�㣬CDƽ�֡�ACB��AB�ڵ�D�������в�����ͼ��
����1���ֱ��Ե�C�͵�DΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ��M��N���㣻
�ij�Ϊ�뾶�����������ཻ��M��N���㣻
����2����ֱ��MN���ֱ�AC��BC�ڵ�E��F��
����3������DE��DF��
��AC=4��BC=2�����߶�DE�ij�Ϊ![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯��һ�δ���ȫ����������֪ʶ���������30��ͬѧ�μ���ξ������ɼ��ֲ�Ƶ�������£�(��λ����)
�ɼ�(��) | ����ֵ | Ƶ��(����) |
80.5~85.5 | 83 | 3 |
85.5~90.5 | 88 | 6 |
90.5~95.5 | 93 | 12 |
95.5~100.5 | 98 | 9 |
��1����������ֵ������30λͬѧ��ƽ������
��2��ѧУ������ξ����ɼ��Ӹߵ���ѡ15λͬѧ�μ��м�������С��ͬѧҲ�μ�����ξ�����֪���Լ��ijɼ�������֪���Լ��Ƿ����ʸ�μ��������(ѧУ��δ�����������������)������Ӧ��עƵ����ƽ���֣���������λ���е��ĸ�������˵�����ɣ�
��3��������֪ʶ�������У���һ�Ƚ���С��ͬѧ�õ���ӡ�й��ȡ���ֽ���ʵ�ͼ������ö�����£�������ѡȡ��ö���ܵܣ���С�����ܵܵ���ö�������У�ǡ���вʵ�ͼ���ĸ����Ƕ��٣�������״ͼ���б���˵����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com