
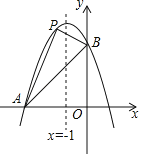
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)△PAB的面积的最大值为![]() ,此时点P的坐标(
,此时点P的坐标(![]() ,
,![]() ).
).
【解析】
(1)因为对称轴是直线x=-1,所以得到点A(-3,0)的对称点是(1,0),因此利用交点式y=a(x-x1)(x-x2),求出解析式.
(2)根据面积的和差,可得二次函数,根据二次函数的性质,可得最大值,根据自变量与函数值的对应关系,可得答案.
(1)∵抛物线对称轴是直线x=﹣1且经过点A(﹣3,0)
由抛物线的对称性可知:抛物线还经过点(1,0)
设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0)
即:y=a(x﹣1)(x+3)
把B(0,3)代入得:3=﹣3a
∴a=﹣1
∴抛物线的解析式为:y=﹣x2﹣2x+3.
(2)设直线AB的解析式为y=kx+b,
∵A(﹣3,0),B(0,3),
∴![]() ,
,
∴直线AB为y=x+3,
作PQ⊥x轴于Q,交直线AB于M,
设P(x,﹣x2﹣2x+3),则M(x,x+3),
∴PM=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴△PAB的面积的最大值为![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,
,![]() ).
).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)从中任取一张,求取到偶数的概率.
(2)甲、乙两人进行摸牌游戏.
①甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
②若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面倒扣着背面图案相同的四张卡片,其正面分别标记有数字![]() ,先任意抽取一张,卡片上的数记作x,不放回,再抽取一张,卡片上的数字记作y,设点A的坐标为(x,y).
,先任意抽取一张,卡片上的数记作x,不放回,再抽取一张,卡片上的数字记作y,设点A的坐标为(x,y).
(1)用树状图或列表法列举点A所有的坐标情况;
(2)求点A在抛物线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点A的坐标为(﹣3,4).
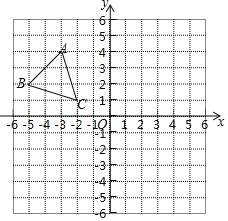
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1的坐标;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2,并写出A2的坐标;
(3)求出(2)中点A所经过的路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)求从中任意抽取1个球恰好是红球的概率;
(2)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙,你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
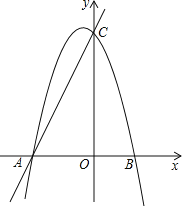
【题目】如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=﹣x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=﹣![]() 时,y取最大值
时,y取最大值![]() .
.
(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)若直线y=![]() x+a与(1)中所求的抛物线交于M、N两点,问:
x+a与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>90°时,a的取值范围(不写过程,直接写结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
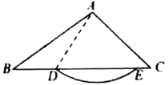
【题目】在![]() 中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称
中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称![]() 为
为![]() 的A-外截弧.例如,图中
的A-外截弧.例如,图中![]() 是
是![]() 的一条A-外截弧.在平面直角坐标系xOy中,已知
的一条A-外截弧.在平面直角坐标系xOy中,已知![]() 存在A-外截弧,其中点A的坐标为
存在A-外截弧,其中点A的坐标为![]() ,点B与坐标原点O重合.
,点B与坐标原点O重合.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,满足条件的点C是_______.
中,满足条件的点C是_______.
(2)若点C在直线![]() 上.
上.
①求点C的纵坐标的取值范围.
②直接写出![]() 的A-外截弧所在圆的半径r的取值范围.
的A-外截弧所在圆的半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com