
”¾ĢāÄæ”æ¶ØŅå£ŗÓŠĮ½Ģõ±ß³¤µÄ±ČÖµĪŖ![]() µÄÖ±½ĒČż½ĒŠĪ½Š×ö”°÷ČĮ¦Čż½ĒŠĪ”±ĪŅĆĒÖŖµĄ£¬ĆüĢā”°Ö±½ĒČż½ĒŠĪ30”ć½ĒĖł¶ŌµÄÖ±½Ē±ßµČÓŚŠ±±ßµÄŅ»°ė”±ŹĒŅ»øöÕęĆüĢā£¬ĖłŅŌ”°ŗ¬30”ć½ĒµÄÖ±½ĒČż½ĒŠĪ”±¾ĶŹĒŅ»øö”°÷ČĮ¦Čż½ĒŠĪ”±
µÄÖ±½ĒČż½ĒŠĪ½Š×ö”°÷ČĮ¦Čż½ĒŠĪ”±ĪŅĆĒÖŖµĄ£¬ĆüĢā”°Ö±½ĒČż½ĒŠĪ30”ć½ĒĖł¶ŌµÄÖ±½Ē±ßµČÓŚŠ±±ßµÄŅ»°ė”±ŹĒŅ»øöÕęĆüĢā£¬ĖłŅŌ”°ŗ¬30”ć½ĒµÄÖ±½ĒČż½ĒŠĪ”±¾ĶŹĒŅ»øö”°÷ČĮ¦Čż½ĒŠĪ”±
£Ø1£©Éč”°÷ČĮ¦Čż½ĒŠĪ”±½Ļ¶ĢÖ±½Ē±ßĪŖa£¬½Ļ³¤Ö±½Ē±ßĪŖb£¬ĒėÄćÖ±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
£Ø2£©ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻB£½90”ć£¬BC£½6£¬DŹĒABµÄÖŠµć£¬µćEŌŚCDÉĻ£¬Āś×ćAD£½DE£¬Į¬½įAE£¬¹żµćD×÷DF”ĪAE½»BCÓŚµćF
¢ŁČē¹ūµćEŹĒCDµÄÖŠµć£¬ĒóÖ¤£ŗ”÷BDFŹĒ”°÷ČĮ¦Čż½ĒŠĪ”±
¢ŚČē¹ū”÷BDFŹĒ”°÷ČĮ¦Čż½ĒŠĪ”±£¬ĒŅBF£½![]() BC£¬ĒóĻ߶ĪACµÄ³¤
BC£¬ĒóĻ߶ĪACµÄ³¤
£Ø¶ž“ĪøłŹ½ŌĖĖćĢįŹ¾£ŗ£Ø![]() £©2£½n2£Ø
£©2£½n2£Ø![]() £©2£½n2a£¬±ČČē£ŗ£Ø4
£©2£½n2a£¬±ČČē£ŗ£Ø4![]() £©2£½42
£©2£½42![]() £Ø
£Ø![]() £©2£½16”Į3£½48£©
£©2£½16”Į3£½48£©

”¾“š°ø”æ£Ø1£©![]() »ņ2;£Ø2£©¢Ł¼ū½āĪö;¢ŚACµÄ³¤ĪŖ2
»ņ2;£Ø2£©¢Ł¼ū½āĪö;¢ŚACµÄ³¤ĪŖ2![]() »ņ10»ņ2
»ņ10»ņ2![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©É花±ß³¤ĪŖc£¬·ÖĮ½ÖÖĒéæö¢Łµ±![]() Ź±£¬c=2a£¬Óɹ“¹É¶ØĄķĒó³öb£¬¼“æÉµĆ³ö
Ź±£¬c=2a£¬Óɹ“¹É¶ØĄķĒó³öb£¬¼“æÉµĆ³ö![]() µÄÖµ£»
掙术
¢Śµ±![]() Ź±£¬b=2a£¬¼“æÉµĆ³ö
Ź±£¬b=2a£¬¼“æÉµĆ³ö![]() µÄÖµ£»
掙术
£Ø2£©¢ŁÖ¤³ö”ĻBCD=30”ć£¬µĆ³ö”ĻBDC=60”ć£¬ÓÉĘ½ŠŠĻߵĊŌÖŹŗĶµČŃüČż½ĒŠĪµÄŠŌÖŹµĆ³ö”ĻEDF=”ĻBDF=30”ć£¬ÓÉÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆ³öBF=![]() DF£¬¼“æÉµĆ³ö½įĀŪ£»
DF£¬¼“æÉµĆ³ö½įĀŪ£»
¢Ś·ÖĖÄÖÖĒéæö µ±![]() =
=![]() Ź±£¬Ēó³öBD=
Ź±£¬Ēó³öBD=![]() BF=1£¬µĆ³öAB=2BD=2£¬Óɹ“¹É¶ØĄķµĆ³öAC=
BF=1£¬µĆ³öAB=2BD=2£¬Óɹ“¹É¶ØĄķµĆ³öAC=![]() =2
=2![]() £»
£»
µ±![]() =
=![]() Ź±£¬Ēó³öBD=2BF=4£¬µĆ³öAB=2BD=8£¬Óɹ“¹É¶ØĄķAC=
Ź±£¬Ēó³öBD=2BF=4£¬µĆ³öAB=2BD=8£¬Óɹ“¹É¶ØĄķAC=![]() =10£»
=10£»
µ±![]() =
=![]() Ź±£¬Ēó³öDF=2BF=4£¬Óɹ“¹É¶ØĄķµĆ³öBD=
Ź±£¬Ēó³öDF=2BF=4£¬Óɹ“¹É¶ØĄķµĆ³öBD=![]() =2
=2![]() £¬µĆ³öAB=2BD=4
£¬µĆ³öAB=2BD=4![]() £¬Óɹ“¹É¶ØĄķµĆ³öAC=
£¬Óɹ“¹É¶ØĄķµĆ³öAC=![]() =2
=2![]() £»
£»
µ±![]() =
=![]() Ź±£¬Óɹ“¹É¶ØĄķĒó³öBD=
Ź±£¬Óɹ“¹É¶ØĄķĒó³öBD=![]() £¬µĆ³öAB=2BD=
£¬µĆ³öAB=2BD=![]() £¬Óɹ“¹É¶ØĄķµĆ³öAC=
£¬Óɹ“¹É¶ØĄķµĆ³öAC=![]() =
=![]() ¼“æÉ£®
¼“æÉ£®
£Ø1£©½ā£ŗÉ花±ß³¤ĪŖc£¬·ÖĮ½ÖÖĒéæö£ŗ
¢Łµ±![]() Ź±£¬c£½2a£¬
Ź±£¬c£½2a£¬
Ōņb£½![]() £¬
£¬
”ą![]() £½
£½![]() £½
£½![]() £»
£»
¢Śµ±![]() Ź±£¬b£½2a£¬
Ź±£¬b£½2a£¬
”ą![]() £½2£»
£½2£»
×ŪÉĻĖłŹö£¬![]() µÄÖµĪŖ
µÄÖµĪŖ![]() »ņ2£»
»ņ2£»
£Ø2£©¢ŁÖ¤Ć÷£ŗ”ßDŹĒABµÄÖŠµć£¬
”ąAD£½BD£¬
”ßAD£½DE£¬
”ąBD£½DE£¬
”ßµćEŹĒCDµÄÖŠµć£¬
”ąDE£½![]() CD£¬
CD£¬
”ąBD£½![]() CD£¬
CD£¬
”ß”ĻB£½90”ć£¬
”ą”ĻBCD£½30”ć£¬
”ą”ĻBDC£½60”ć£¬
”ßDF”ĪAE£¬
”ą”ĻDEA£½”ĻEDF£¬”ĻDAE£½”ĻBDF£¬
”ßAD£½DE£¬
”ą”ĻDAE£½”ĻDEA£¬
”ą”ĻEDF£½”ĻBDF£½30”ć£¬
”ąBF£½![]() DF£¬
DF£¬
”ą![]() £½
£½![]() £¬
£¬
”ą”÷BDFŹĒ”°÷ČĮ¦Čż½ĒŠĪ”±£»
¢Ś½ā£ŗ·ÖĖÄÖÖĒéæö£ŗ
µ±![]() =
=![]() Ź±£¬
Ź±£¬
”ßBF£½![]() BC£¬BC£½6£¬
BC£¬BC£½6£¬
”ąBF£½2£¬
”ąBD£½![]() BF£½1£¬
BF£½1£¬
”ßDŹĒABµÄÖŠµć£¬
”ąAB£½2BD£½2£¬
”ąAC£½![]() £½
£½![]() £½2
£½2![]() £»
£»
µ±![]() =
=![]() Ź±£¬
Ź±£¬
”ßBF£½![]() BC£¬BC£½6£¬
BC£¬BC£½6£¬
”ąBF£½2£¬
”ąBD£½2BF£½4£¬
”ßDŹĒABµÄÖŠµć£¬
”ąAB£½2BD£½8£¬
”ąAC£½![]() £½
£½![]() £½10£»
£½10£»
µ±![]() =
=![]() Ź±£¬
Ź±£¬
”ßBF£½![]() BC£¬BC£½6£¬
BC£¬BC£½6£¬
”ąBF£½2£¬
”ąDF£½2BF£½4£¬
”ąBD=![]() =
=![]() =2
=2![]() £¬
£¬
”ßDŹĒABµÄÖŠµć£¬
”ąAB£½2BD£½4![]() £¬
£¬
”ąAC=![]() =2
=2![]() £»
£»
µ±![]() =
=![]() Ź±£¬
Ź±£¬
”ąDF£½2BD£¬
”ßBF£½![]() BC£¬BC£½6£¬
BC£¬BC£½6£¬
”ąBF£½2£¬
Óɹ“¹É¶ØĄķµĆ£ŗDF2©BD2£½BF2£¬¼“£Ø2BD£©2©BD2£½22£¬
½āµĆ£ŗBD=![]() £¬
£¬
”ąAB£½2BD£½![]() £¬
£¬
”ąAC£½![]()
£½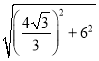 £½
£½![]() £»
£»
×ŪÉĻĖłŹö£¬Čē¹ū”÷BDFŹĒ”°÷ČĮ¦Čż½ĒŠĪ”±£¬ĒŅBF£½![]() BC£¬Ļ߶ĪACµÄ³¤ĪŖ2
BC£¬Ļ߶ĪACµÄ³¤ĪŖ2![]() »ņ10»ņ2
»ņ10»ņ2![]() »ņ
»ņ![]() £®
£®


 ĮĮµć¼¤»ī¾«±ąĢįÓÅ100·Ö“óŹŌ¾ķĻµĮŠ“š°ø
ĮĮµć¼¤»ī¾«±ąĢįÓÅ100·Ö“óŹŌ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
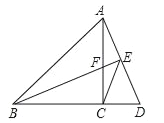
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AC=BC£¬”ĻACB=90”ć£¬µćDŌŚBCµÄŃÓ³¤ĻßÉĻ£¬Į¬½ÓAD£¬¹żB×÷BE”ĶAD£¬“¹×ćĪŖE£¬½»ACÓŚµćF£¬Į¬½ÓCE£®
£Ø1£©ĒóÖ¤£ŗ”÷BCF”Õ”÷ACD£®
£Ø2£©²ĀĻė”ĻBECµÄ¶ČŹż£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©Ģ½¾æĻ߶ĪAE£¬BE£¬CEÖ®¼äĀś×ćµÄµČĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
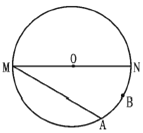
”¾ĢāÄæ”æČēĶ¼£¬MNŹĒ”ŃOµÄÖ±¾¶£¬MN=4£¬µćAŌŚ”ŃOÉĻ£¬”ĻAMN=30”ć£¬BĪŖ![]() µÄÖŠµć£¬PŹĒÖ±¾¶MNÉĻŅ»¶Æµć.
µÄÖŠµć£¬PŹĒÖ±¾¶MNÉĻŅ»¶Æµć.
(1)ĄūÓĆ³ß¹ę×÷Ķ¼£¬Č·¶Øµ±PA+PB×īŠ”Ź±PµćµÄĪ»ÖĆ(²»Š“×÷·Ø£¬µ«ŅŖ±£Įō×÷Ķ¼ŗŪ¼£).
(2)ĒóPA+PBµÄ×īŠ”Öµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=![]() £Ø
£Ø![]() £©£¬½«Ļ߶ĪBCČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪBD”£
£©£¬½«Ļ߶ĪBCČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪBD”£

£Ø1£©ČēĶ¼1£¬Ö±½ÓŠ“³ö”ĻABDµÄ“󊔣ØÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾£©£»
µÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©ČēĶ¼2£¬”ĻBCE=150”ć£¬”ĻABE=60”ć£¬ÅŠ¶Ļ”÷ABEµÄŠĪד²¢¼ÓŅŌÖ¤Ć÷£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½įDE£¬Čō”ĻDEC=45”ć£¬Ēó![]() µÄÖµ”£
µÄÖµ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöÕżÕūŹż£¬ÓÉNøöŹż×Ö×é³É£¬ČōĖüµÄµŚŅ»Ī»ŹżæÉŅŌ±»1Õū³ż£¬ĖüµÄĒ°Į½Ī»ŹżæÉŅŌ±»2Õū³ż£¬Ē°ČżĪ»ŹżæÉŅŌ±»3Õū³ż£¬”£¬Ņ»Ö±µ½Ē°NĪ»ŹżæÉŅŌ±»NÕū³ż£¬ŌņÕāŃłµÄŹż½Š×ö”°¾«ĒÉŹż”±£®Čē£ŗ123µÄµŚŅ»Ī»Źż”°1”±æÉŅŌ±»1Õū³ż£¬Ē°Į½Ī»Źż”°12”±æÉŅŌ±»2Õū³ż£¬”°123”±æÉŅŌ±»3Õū³ż£¬Ōņ123ŹĒŅ»øö”°¾«ĒÉŹż”±£®
£Ø1£©ČōĖÄĪ»Źż![]() ŹĒŅ»øö”°¾«ĒÉŹż”±£¬ĒókµÄÖµ£»
ŹĒŅ»øö”°¾«ĒÉŹż”±£¬ĒókµÄÖµ£»
£Ø2£©ČōŅ»øöČżĪ»”°¾«ĒÉŹż”±![]() ø÷Ī»Źż×ÖÖ®ŗĶĪŖŅ»øöĶźČ«Ę½·½Źż£¬ĒėĒó³öĖłÓŠĀś×ćĢõ¼žµÄČżĪ»”°¾«ĒÉŹż”±£®
ø÷Ī»Źż×ÖÖ®ŗĶĪŖŅ»øöĶźČ«Ę½·½Źż£¬ĒėĒó³öĖłÓŠĀś×ćĢõ¼žµÄČżĪ»”°¾«ĒÉŹż”±£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µČ±ß”÷ABCµÄ±ß³¤ĪŖ2£¬¹żµćBµÄÖ±Ļß![]() ĒŅ”÷ABCÓė”÷A”äBC”ä¹ŲÓŚÖ±Ļßl¶Ō³Ę£¬DĪŖĻ߶ĪBC”äÉĻŅ»¶Æµć£¬ŌņAD+CDµÄ×īŠ”ÖµŹĒ____.
ĒŅ”÷ABCÓė”÷A”äBC”ä¹ŲÓŚÖ±Ļßl¶Ō³Ę£¬DĪŖĻ߶ĪBC”äÉĻŅ»¶Æµć£¬ŌņAD+CDµÄ×īŠ”ÖµŹĒ____.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻߵĶ„µć×ų±źĪŖC£Ø0£¬8£©£¬²¢ĒŅ¾¹żA£Ø8£¬0£©£¬µćPŹĒÅ×ĪļĻßÉĻµćA£¬C¼äµÄŅ»øö¶Æµć£Øŗ¬¶Ėµć£©£¬¹żµćP×÷Ö±Ļßy=8µÄ“¹Ļߣ¬“¹×ćĪŖµćF£¬µćD£¬EµÄ×ų±ź·Ö±šĪŖ£Ø0£¬6£©£¬£Ø4£¬0£©£¬Į¬½ÓPD£¬PE£¬DE£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©²ĀĻė²¢Ģ½¾æ£ŗ¶ŌÓŚČĪŅāŅ»µćP£¬PDÓėPFµÄ²īŹĒ·ńĪŖ¹Ģ¶ØÖµ£æČē¹ūŹĒ£¬ĒėĒó³ö“Ė¶ØÖµ£»Čē¹ū²»ŹĒ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©Ēó£ŗ¢Łµ±”÷PDEµÄÖܳ¤×īŠ”Ź±µÄµćP×ų±ź£»¢ŚŹ¹”÷PDEµÄĆ껿ĪŖÕūŹżµÄµćPµÄøöŹż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży£½ax2£«bx£«cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
(1)Š“³ö·½³Ģax2£«bx£«c£½0µÄĮ½øöøł£»
(2)µ±xĪŖŗĪÖµŹ±£¬y£¾0£æµ±xĪŖŗĪÖµŹ±£¬y£¼0?
(3)Š“³öyĖęxµÄŌö“ó¶ų¼õŠ”µÄ×Ō±äĮæxµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ±±¾©ŹĄ½ēŌ°ŅÕ²©ĄĄ»į£Ø¼ņ³Ę”°ŹĄŌ°»į”±£©Ō°Ēų2019Äź4ŌĀ29ČÕÖĮ2019Äź10ŌĀ7ČÕŌŚÖŠ¹ś±±¾©ŹŠŃÓĒģĒų¾ŁŠŠ£¬ĆÅʱ¼ŪøńČē±ķ£ŗŠ”Ć÷Č«¼ŅÓŚ9ŌĀ28ČÕ¼ÆĢåČėŌ°²Ī¹ŪÓĪĄĄ£¬Ķعż¼ĘĖć·¢ĻÖ£ŗČōĢįĒ°Į½ĢģĻßÉĻ¹ŗĀņĆÅʱĖłŠč·ŃÓĆĪŖ996ŌŖ£¬¶ųČėŌ°µ±Ģģ¹ŗʱĖłŠč·ŃÓĆĪŖ1080ŌŖ£¬ŌņøĆ¼ŅĶ„ÖŠæÉŅŌ¹ŗĀņÓÅ»ŻĘ±µÄÓŠ_____ČĖ£®
ʱÖÖ | ʱ¼Ū£ØŌŖ/ČĖ£© | |
Öø¶ØČÕ | ĘÕĶØʱ | 160 |
ÓÅ»ŻĘ± | 100 | |
Ę½ČÕ | ĘÕĶØʱ | 120 |
ÓÅ»ŻĘ± | 80 | |
×¢1£ŗ”°Öø¶ØČÕ”±ĪŖæŖŌ°ČÕ£Ø4ŌĀ29ČÕ£©”¢ĪåŅ»ĄĶ¶Æ½Ś£Ø5ŌĀ1ČÕ£©”¢¶ĖĪē½Ś”¢ÖŠĒļ½Ś”¢Ź®Ņ»¼ŁĘŚ£Øŗ¬±ÕŌ°ČÕ£©£¬”°Ę½ČÕ”±ĪŖŹĄŌ°»į»įĘŚ³ż”°Öø¶ØČÕ”±ĶāµÄĘäĖūČÕĘŚ£»
×¢2£ŗĮłŹ®ÖÜĖź¼°ŅŌÉĻĄĻČĖ”¢Ź®°ĖÖÜĖźŅŌĻĀµÄѧɜ¾łæɹŗĀņÓÅ»ŻĘ±£»
×¢3£ŗĢįĒ°Į½Ģģ¼°ŅŌÉĻĻßÉĻ¹ŗĀņŹĄŌ°»įĆÅʱ£¬Ę±¼ŪæÉ“ņ¾ÅÕŪ£¬µ«½öĻŽÓŚĘÕĶØʱ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com