
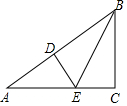
 如图,在△ABC中,∠C=90°,其三边的长之比为3:4:5,按图中的方法将它对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,若不重叠的部分△ADE的面积是6cm2,则△ABC的面积是24或54cm2.
如图,在△ABC中,∠C=90°,其三边的长之比为3:4:5,按图中的方法将它对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,若不重叠的部分△ADE的面积是6cm2,则△ABC的面积是24或54cm2. 分析 分两种情形讨论即可:①当BC:AC:AB=3:4:5时,设BC=3k,AC=4k,AB=5k,则BD=BC=3k,AD=2k,设DE=EC=x,在Rt△ADE中,根据AD2+ED2=AE2,得到4k2+x2=(4k-x)2,得到x=$\frac{3}{2}$k,由$\frac{1}{2}$•AD•DE=6,得$\frac{1}{2}$•2k•$\frac{3}{2}$k=6,可得k2=4,再求出△ABC面积即可.②当BC:AC:AB=4:3:5时,设BC=4k,AC=3k,AB=5k,则BD=BC=4k,AD=k,设DE=EC=x,方法类似.
解答 解:①当BC:AC:AB=3:4:5时,
设BC=3k,AC=4k,AB=5k,则BD=BC=3k,AD=2k,设DE=EC=x,
在Rt△ADE中,∵AD2+ED2=AE2,
∴4k2+x2=(4k-x)2,
∴x=$\frac{3}{2}$k,
∵$\frac{1}{2}$•AD•DE=6,
∴$\frac{1}{2}$•2k•$\frac{3}{2}$k=6,
∴k2=4,
∴S△ABC=$\frac{1}{2}$×3k×4k=6k2=24cm2.
②当BC:AC:AB=4:3:5时,设BC=4k,AC=3k,AB=5k,则BD=BC=4k,AD=k,设DE=EC=x,
在Rt△ADE中,∵AD2+ED2=AE2,
∴k2+x2=(3k-x)2,
∴x=$\frac{4}{3}$k,
∵$\frac{1}{2}$•AD•DE=6,
∴$\frac{1}{2}$•k•$\frac{4}{3}$k=6,
∴k2=9,
∴S△ABC=$\frac{1}{2}$×3k×4k=6k2=54cm.
综上所述,△ABC的面积为24cm2或54cm2.
故答案为24或54.
点评 本题考查翻折变换、直角三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
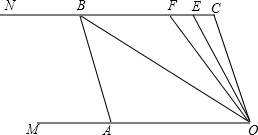 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求完成下列各题:
按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
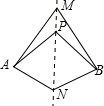 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | ∠ANM=∠BNM | C. | ∠MAP=∠MBP | D. | AP=BN |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O内 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com