
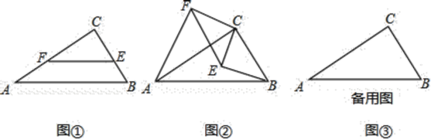
【题目】![]() 尝试探究:如图
尝试探究:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,E,F分别是BC,AC上的点,且
,E,F分别是BC,AC上的点,且![]() ,则
,则![]() ______;
______;
![]() 类比延伸:如图
类比延伸:如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点C顺时针旋转,则在旋转的过程中,
绕点C顺时针旋转,则在旋转的过程中,![]() 值是否发生变化?请仅就图
值是否发生变化?请仅就图![]() 的情形写出推理过程;
的情形写出推理过程;
![]() 拓展运用:若
拓展运用:若![]() ,
,![]() ,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
,在旋转过程中,当B,E,F三点在同一直线上时,请直接写出此时线段AF的长.
【答案】(1)![]() ;(2)不变化,理由见解析;(3)AF的长为3
;(2)不变化,理由见解析;(3)AF的长为3![]() -
-![]() 或3
或3![]() +
+![]() .
.
【解析】
(1)根据直角三角形30°角的性质即可解决问题;
(2)只要证明△ACF∽△BCE,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(3)分两种情形画出图形分别解决问题即可;
(1)如图①中,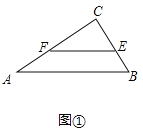
∵在△ABC中,∠ABC=90°,∠A=30°,EF∥AB,
∴∠CFE=∠A=30°,
∴CF=![]() EC,AC=
EC,AC=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC-![]() EC=
EC=![]() (BC-EC)=
(BC-EC)=![]() BE,
BE,
∴![]() =
=![]() ,
,
故答案为![]() .
.
(2)不变化,
理由如下:如图②中,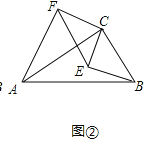
由(1)及旋转的性质知,∠CFE=∠CAB=30°.
∠FCE=∠ACB=90°.
在Rt△CEF中,tan∠CEF=![]() =
=![]() ,
,
在Rt△CBA中,tan∠ABC=![]() =
=![]() ,
,
∴![]() ,
,
又∵∠FCE=∠ACB=90°,∠FCA+∠ACE=∠FCE,
∠ACE+∠BCE=∠ACB,
∴∠FCA=∠ECB.
∴△ACF∽△BCE,
∴![]() =
=![]() .
.
(3)①如图,由△ECB∽△FCA,可得:AF:BE=CF:EC=![]() .
.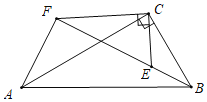
设BE=a,则AF=![]() a,
a,
∵B,E,F共线,
∴∠BEC=∠AFC=120°,
∵∠EFC=30°,
∴∠AFB=90°,
在Rt△ABF中,AB=2BC=6,AF=![]() a,BF=EF+BE=4+a,
a,BF=EF+BE=4+a,
∴(![]() a)2+(4+a)2=62,
a)2+(4+a)2=62,
∴a=-1+![]() 或-1-
或-1-![]() (舍弃),
(舍弃),
∴AF=![]() a=3
a=3![]() -
-![]()
②如图,当E,B,F共线时,同法可证:AF=![]() BE,∠AFB=90°,
BE,∠AFB=90°,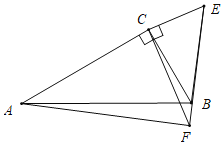
在Rt△ABF中,62=(4-a)2+(![]() a)2,
a)2,
解得a=1+![]() 或1-
或1-![]() (舍弃),
(舍弃),
∴AF=![]() a=3
a=3![]() +
+![]() .
.
AF的长为3![]() -
-![]() 或3
或3![]() +
+![]() .
.


科目:初中数学 来源: 题型:
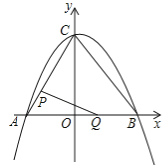
【题目】如图①,在平面直角坐标系中,二次函数y=![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
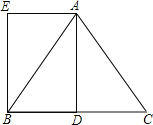
查看答案和解析>>
科目:初中数学 来源: 题型:
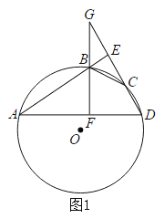
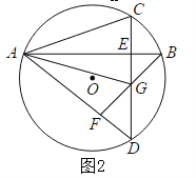
【题目】 AB,CD是![]() 的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作
的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作![]() ,垂足为点F,直线BF交直线CD于点G.
,垂足为点F,直线BF交直线CD于点G.
(1)如图1当点E在![]() 外时,连接
外时,连接![]() ,求证BE平分∠GBC;
,求证BE平分∠GBC;
(2)如图2当点E在![]() 内时,连接AC,AG,求证:AC=AG
内时,连接AC,AG,求证:AC=AG
(3)在(2)条件下,连接BO,若BO平分![]() ,求线段EC的长.
,求线段EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=1,记∠ABC=α,点D为射线BC上的动点,连接AD,将射线DA绕点D顺时针旋转α角后得到射线DE,过点A作AD的垂线,与射线DE交于点P,点B关于点D的对称点为Q,连接PQ.
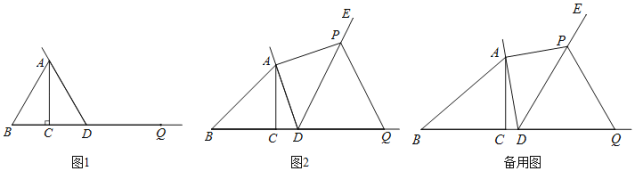
(1)当△ABD为等边三角形时,
①依题意补全图1;
②PQ的长为 ;
(2)如图2,当α=45°,且BD=![]() 时,求证:PD=PQ;
时,求证:PD=PQ;
(3)设BC=t,当PD=PQ时,直接写出BD的长.(用含t的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
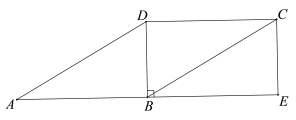
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M(﹣1,![]() ),N(1,
),N(1,![]() )是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
)是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
(1)在点![]() ,
,![]() ,
,![]() ,A4(2,2)中,线段MN的可视点为 ;
,A4(2,2)中,线段MN的可视点为 ;
(2)若点B是直线y=x![]() 上线段MN的可视点,求点B的横坐标t的取值范围;
上线段MN的可视点,求点B的横坐标t的取值范围;
(3)直线y=x+b(b≠0)与x轴交于点C,与y轴交于点D,若线段CD上存在线段MN的可视点,直接写出b的取值范围.
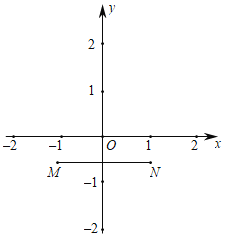
查看答案和解析>>
科目:初中数学 来源: 题型:
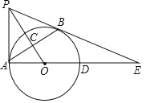
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
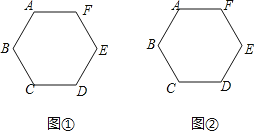
【题目】如图,已知多边形ABCDEF中,AB=AF,DC=DE,BC=EF,∠ABC=∠BCD.请仅用无刻度的直尺,分别按下列要求画图.
(1)在图①中,画出一个以BC为边的矩形;
(2)在图②中,若多边形ABCDEF是正六边形,试在AF上画出点M,使得AM=![]() AF.
AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com