
| ||
| 2 |
| 3 |
 解:(1)AF=4
解:(1)AF=4| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
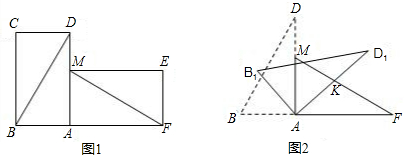
有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.

1.在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
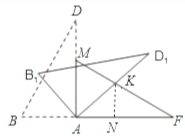
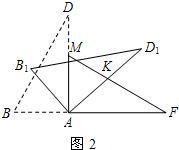
2.小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;

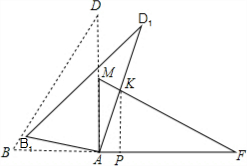
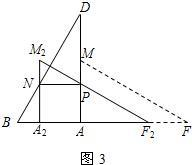
3.若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京门头沟中考二模数学试卷(解析版) 题型:解答题
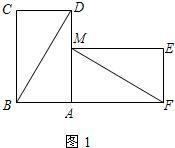
有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.

1.在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
2.小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;

3.若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com