Question

17．乘法公式的探究及应用．
（1）如左图，可以求出阴影部分的面积是a²-b²（写成两数平方差的形式）；若将阴影部分裁剪下来，重新拼成一个矩形，如右图，它的面积是（a+b）（a-b）（写成多项式乘法的形式），比较左、右两图的阴影部分的面积，可以得到乘法公式（a+b）（a-b）=a²-b²（用式子表达）
（2）运用你所得到的公式，计算：100.3×99.7．

Answer 1

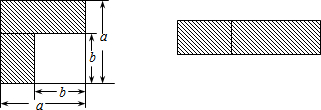
分析 （1）根据左图与右图，分别确定出阴影部分面积，得出乘法公式即可；
（2）利用得出的公式将原式变形，计算即可得到结果．

解答 解：（1）如左图，可以求出阴影部分的面积是a²-b²（写成两数平方差的形式）；
若将阴影部分裁剪下来，重新拼成一个矩形，如右图，它的面积是（a+b）（a-b）（写成多项式乘法的形式），
比较左、右两图的阴影部分的面积，可以得到乘法公式（a+b）（a-b）=a²-b²（用式子表达）；
故答案为：a²-b²；（a+b）（a-b）；（a+b）（a-b）=a²-b²；
（2）根据题意得：原式=（100+0.3）×（100-0.3）=10000-0.9=9999.1．

点评 此题考查了平方差公式的几何背景，表示出图形阴影部分面积是解题的关键．