【题目】如图，A和B两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A的速度每分钟增加6米，则A和B在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取π=3.14）
【答案】圆周直径至多是28米，至少是10米
【解析】试题分析：行程中的相遇问题，从小学开始就是重要的应用题型，属基本题型．其中路程、时间与速度的关系是基本知识．
试题解析：由于圆的直径为D，则圆周长为πD．设A和B的速度和是每分钟v米，一次相遇所用的时间为
分；他们15分钟内相遇7次，用数学语言可以描述为
如果A的速度每分钟增加6米，A加速后的两个机器人的速度和是每分钟（v+6）米，则A和B在15分钟内相遇9次，用数学语言可以描述为
本题不是列方程，而是列不等式来描述题设的数量关系，这对一般学生可能比较生疏，体现了基本技能的灵活性．
由①，得
， 由②，得
上面两式相加，则有
，28.6624＞D＞9.55414，29＞D＞9．
已知“圆的直径为整数米”，所以，圆周直径至多是28米，至少是10米．
阅读快车系列答案科目：初中数学 来源： 题型：
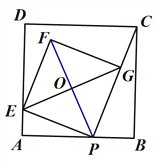
【题目】如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以PE为边作正方形PEFG，顶点G在线段PC上. 对角线EG、FP相交于点O.
（1）若AP=3，求AE的长；
（2）连接AC，判断点O是否在AC上，并说明理由；
（3）在点P从点A到点B的运动过程中，正方形PEFG也随之运动，求DE的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴的单位长度为1．
（1）如果点A、D表示的数互为相反数，那么点B表示的数是多少？
（2）当点B为原点时，若存在一点M到A点的距离是点M到D点的距离的2倍，则点M所表示的数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，对角线AC、BD相交于点O，且OA=OB
（1）求证：四边形ABCD是矩形；
（2）若AB=5，∠AOB=60°，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2011贵州安顺，17，4分）已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为 ．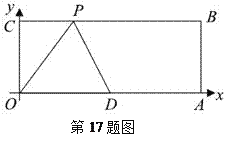
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG。求证：①∠BEA =∠G，② EF=FG。
（2）如图2，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：
（1）小明总共剪开了_______条棱．
（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．
（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．
查看答案和解析>>
科目：初中数学 来源： 题型：
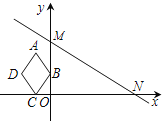
【题目】如图,在直角坐标系中,菱形ABCD的顶点坐标C(-1,0)、B(0,2)、D(n,2),点A在第二象限.直线y=-
x+5与x轴、y轴分别交于点N、M.将菱形ABCD沿x轴向右平移m个单位.当点A落在MN上时，则m+n= ________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
