



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
 22、定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
22、定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山九年级上学期期末考试数学试卷(解析版) 题型:解答题
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
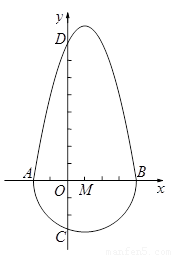
(1)请你直接写出“蛋圆”抛物线部分的解析式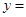 ,自变量的取值范围是
;
,自变量的取值范围是
;
(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
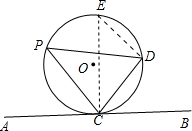
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com