
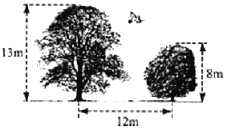
【题目】如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
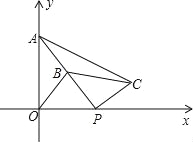
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证:![]() 是等边三角形.
是等边三角形.
(![]() )点
)点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,作
,作![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() .
.
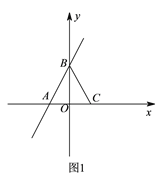
①如图![]() ,若
,若![]() ,直接写出
,直接写出![]() 的度数.
的度数.
②若点![]() 在线段
在线段![]() 的延长线上运动(
的延长线上运动(![]() 与点
与点![]() 不重合),
不重合),![]() 的度数是否变化?若变化,请说明理由;若不变,求出
的度数是否变化?若变化,请说明理由;若不变,求出![]() 的度数.
的度数.
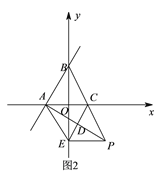
(![]() )在(
)在(![]() )的条件下,若点
)的条件下,若点![]() 从点
从点![]() 出发在
出发在![]() 的延长线上匀速运动,速度为每秒
的延长线上匀速运动,速度为每秒![]() 个单位长度,
个单位长度,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,运动时间为
,运动时间为![]() 秒时.求
秒时.求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
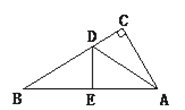
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com