
【题目】如图,一次函数![]() =
=![]() 的图像与正比例函数
的图像与正比例函数![]() =
=![]() 的图像相交于点A(2,
的图像相交于点A(2,![]() ),与
),与![]() 轴相交于点B.
轴相交于点B.

(1)求![]() 、
、![]() 的值;
的值;
(2)在![]() 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
【答案】(1)a=1,b=2;(2)点C的坐标为(0,2)或(0,-2).
【解析】
(1)利用正比例函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标,利用待定系数法即可求出b的值;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,根据三角形的面积公式结合△AOC的面积等于△AOB的面积,即可得出点C的坐标.
解:(1)把点A(2,a)的坐标代入y=![]() x,解得a=1.
x,解得a=1.
把点A(2,1)的坐标代入y=-![]() x+b,解得b=2.
x+b,解得b=2.
(2)把y=0代入y=-![]() x+2,解得x=4.
x+2,解得x=4.
∴点B的坐标为(4,0).
∴OB=4.
∵S△AOC=S△AOB,
∴![]() ×2·OC=
×2·OC=![]() ×4×1.
×4×1.
∴OC=2.
∴点C的坐标为(0,2)或(0,-2).


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
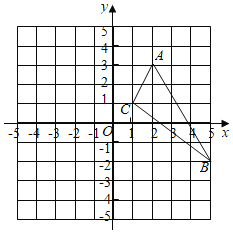
【题目】已知如图,在![]() 中,三个顶点的坐标分别为
中,三个顶点的坐标分别为![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,其 中点
,其 中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]()
![]() 直接写出平移后的
直接写出平移后的![]() 的顶点坐标:
的顶点坐标:
![]()
![]()
![]()
![]() 在坐标系中画出平移后的
在坐标系中画出平移后的![]()
![]() 求出
求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)若∠1=∠2,试说明DG∥BC.
(2)若CD 平分∠ACB,∠A=60°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,cos∠ABC= ![]() ,sin∠ACB=
,sin∠ACB= ![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 .
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称____ ___,___ ;(2分)
(2)如图,已知格点(小正方形的顶点)![]() ,
,![]() ,
,![]() ,请你直接写出所有以格点为顶点,
,请你直接写出所有以格点为顶点,![]() 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形![]() 的顶点M的坐标。(3分)
的顶点M的坐标。(3分)

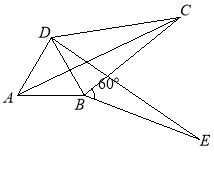
(3)如图,将![]() 绕顶点
绕顶点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连结
,连结![]() ,
,![]() .求证:
.求证:![]() ,即四边形
,即四边形![]() 是勾股四边形.(4分)
是勾股四边形.(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 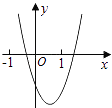
A.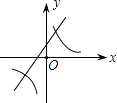
B.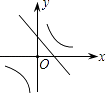
C.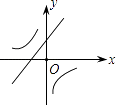
D.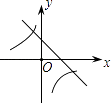
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com