
(11·大连)(本题12分)如图15,抛物线y=ax2+bx+c经过A(-1,0)、B (3,
0)、C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)抛物线上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相
等,若存在,直接写出点R的坐标;若不存在,说明理由.
解:(1)设抛物线解析式为y=a(x+1)(x-3)
∴3=a·(-3) 即=a-1
∴所求的解析式为y=-(x+1)(x-3)=-x2+2x+3…………………………2分
解法二:把三点代入抛物线解析式y=ax2+bx+c,
∴所求的解析式为y=-(x+1)(x-3)=-x2+2x+3…………………………2分
(2)存在
y=-x2+2x+3=-(x-1)2+4 ∴点P的坐标为 (1,4)
设直线BC的解析式为y=kx+b,
即y=-x+3
∴点M的坐标为 (1,2) …………………………3分
设对称轴与x轴相交于点N,则MN=PM,
∴△NMB与△PMB的面积相等
∴△QMB与△PMB的面积相等
∴点Q在过点P且平行于BC的直线l1或过点N且平行于BC的直线l2上,
设l1的解析式为y=-x+b1,则4=-1+b1,b1=5,∴y=-x+5
设l2的解析式为y=-x+b2,则0=-1+b2,b2=1,∴y=-x+1………………………6分
设l1与抛物线相交于点Q (m,-m+5) l2与抛物线相交于点Q’ (n,-n+1)
-m+5=-m2+2m+3 解得m1=1(舍去),m2=2,∴Q (2,3) ……………………7分
-n+1=-n2+2n+3
解析:略


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
(11·大连)(本题12分)在△ABC中,∠A=90°,点D在线段BC上,∠EDB
=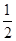 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
(1)当AB=AC时,(如图13),
① ∠EBF=_______°;
② 探究线段BE与FD的数量关系,并加以证明;
(2)当AB=kAC时(如图14),求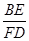 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·大连)(本题11分)如图,在平面直角坐标系中,点A、B、C的坐标分别
为(0,2)、(-1,0)、(4,0).P是线段OC上的一动点(点P与点O、C不重合),过点P
的直线x=t与AC相交于点Q.设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
部分的面积为S.
(1)点B关于直线x=t的对称点B′的坐标为________;
(2)求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·大连)(本题10分)如图10,某容器由A、B、C三个长方体组成,其中
A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的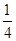 (容器各面的厚
(容器各面的厚
度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图11是注水
全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.
⑴在注水过程中,注满A所用时间为______s,再注满B又用了_____s;
⑵求A的高度hA及注水的速度v;
⑶求注满容器所需时间及容器的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·大连)(本题9分)如图9,AB是⊙O的直径,CD是⊙O的切线,切点
为C,BE⊥CD,垂足为E,连接AC、BC.
(1)△ABC的形状是______________,理由是_________________;
(2)求证:BC平分∠ABE;
(3)若∠A=60°,OA=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·大连)(本题9分)某中学为了了解七年级男生入学时的跳绳情况,随机
选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数
分布表和部分频数分布直方图(如图8所示).根据图表解答下列问题:
(1)a=_______,b=_________;
(2)这个样本数据的中位数落在第________组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一
人,跳绳成绩为优秀的概率为多少?
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成
绩为优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com