
分析 通过观察我们所要求证的结论,我们很容易想到先把异分母分式变为同分母分式,然后再加减.我们很容易知道这三个分式的公分母是(a-b)(a-c)(b-c),然后对分子、分母同时进行加减化简,最终得到我们要的结论.
解答 证明:∵$\frac{(x+b)(x+c)}{(a-b)(a-c)}$+$\frac{(x+c)(x+a)}{(b-c)(b-a)}$+$\frac{(x+a)(x+b)}{(c-a)(c-b)}$
=$\frac{(x+b)(x+c)(b-c)-(x+c)(x+a)(a-c)+(x+a)(x+b)(a-b)}{(a-b)(a-c)(b-c)}$
=$\frac{{b}^{2}c-b{c}^{2}-{a}^{2}c+a{c}^{2}+{a}^{2}b-a{b}^{2}}{{b}^{2}c-b{c}^{2}-{a}^{2}c+a{c}^{2}+{a}^{2}b-a{b}^{2}}$
=1
∴$\frac{(x+b)(x+c)}{(a-b)(a-c)}+\frac{(x+c)(x+a)}{(b-c)(b-a)}+\frac{(x+a)(x+b)}{(c-a)(c-b)}$=1
点评 本题考查学生对复杂分式化简的掌握,我们可以利用分析法进行证明,先对左边分式进行加减,通过整理化简后得到左边的结果等于1,从而得到我们的结论.


科目:初中数学 来源: 题型:解答题
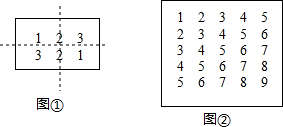
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
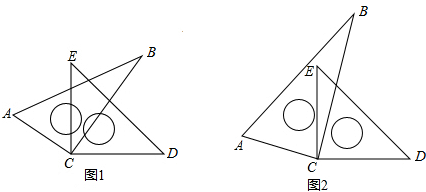
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型号 | 每辆车的座位数 | 每辆车每天的租金(元) |
| A | 10 | 500 |
| B | 20 | 900 |
| C | 30 | 1250 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
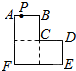 如图,三个大小相同的正方形ABCDEF拼成六边形,一动点P从点A出发沿着A→B→C→D→E方向匀速运动,最后到达点E.运动过程中△PEF的面积(s)随时间(t)变化的图象大致是( )
如图,三个大小相同的正方形ABCDEF拼成六边形,一动点P从点A出发沿着A→B→C→D→E方向匀速运动,最后到达点E.运动过程中△PEF的面积(s)随时间(t)变化的图象大致是( )| A. |  | B. | 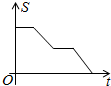 | C. | 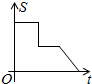 | D. | 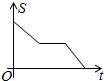 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 分式无意义 | B. | 分式值为0 | ||
| C. | 当a≠$\frac{1}{3}$时,分式的值为0 | D. | a≠$\frac{1}{3}$时,分式的值为0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com