
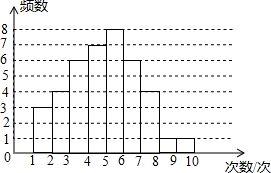
 为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.
为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.分析 (1)把频数直方图中各组的频数相加即可得到所抽取的学生数;
(2)先把直方图中后面5组的频数相加,再计算样本中引体向上次数不低于5次的人数的百分比,然后用800乘以这个百分比可估计出该校九年级学生引体向上次数不低于5次的人数.
解答 解:(1)调查的学生总数为:1+1+3+4+4+6+6+7+8=40(名);
(2)由频数分布直方图得引体向上次数不低于5次的人数为8+6+4+1+1=20(名),
800×$\frac{20}{40}$=400,
所以估计该校九年级学生引体向上次数不低于5次的人数为400人.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了样本估计总体.


科目:初中数学 来源: 题型:解答题
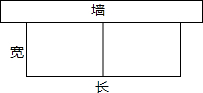 有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:
有长为30m的篱笆,一面利用墙(墙的可用长度不能超过16m)围成一块矩形花圃,如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
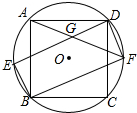 正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com