
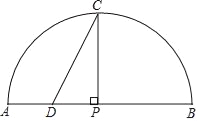
【题目】24如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 |
| 3.2 | 3.4 | 3.3 | 3 |
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为 cm.
【答案】(1)2.9;(2)图像见解析;(3)3.3
【解析】
(1)根据对称性可知:当x=2和x=4时,PA=BP′=2,再根据勾股定理去求解;
(2)利用描点法画出图象即可;
(3)当∠DCP=30°时,CD=2PD,即y=x,再观察图像即可.
解:(1)如图,根据对称性可知:
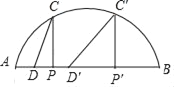
根据对称性可知:当x=2和x=4时,PA=BP′=2,
∵PC⊥AB,P′C′⊥AB,
∴PC=P′C′=![]() ,
,
∴CD=![]() ≈2.9.
≈2.9.
故答案为2.9.
(2)利用描点法画出图象如图所示:
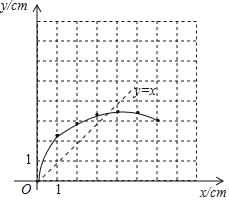
(3)当∠DCP=30°时,CD=2PD,即y=x,
观察图象可知:与函数图象与直线y=x的交点为(3.3,3.3),
∴AP的长度为3.3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
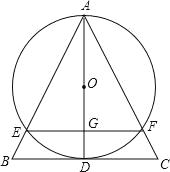
【题目】如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以 AD为直径作⊙O,⊙O分别交AB、AC于 E、F.
(1)求证:BE=CF;
(2)设 AD、EF相交于G,若 EF=8,⊙O的半径为5,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
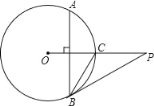
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.

(1)填空:乙的速度v2=________米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张背面完全相同的卡片,它们的正面分别标有数字﹣1,0,1,将他们背面朝上,洗匀后随机抽取一张,把正面的数字作为b,接着再抽取一张,把正面的数字作为c,则满足关于x的一元二次方程x2+bx+c=0有实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0),B(3,0)两点,与y轴交于点C
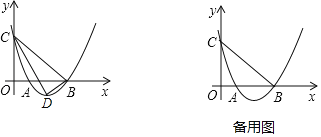
(1)求此二次函数解析式;
(2)点D为抛物线的顶点,试判断△BCD的形状,并说明理由;
(3)将直线BC向上平移t(t>0)个单位,平移后的直线与抛物线交于M,N两点(点M在y轴的右侧),当△AMN为直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x-0.4)成反比例.又知当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com