

分析 (1)直接利用勾股定理得出AC的长;
(2)根据勾股定理画出长为$\sqrt{5}$a、2$\sqrt{2}$a、$\sqrt{17}$a的三角形即可.
(3)根据勾股定理画出长为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$的三角形即可.
解答 解:(1)AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
故答案为:$\sqrt{13}$;
(2)如图2所示:△ABC就是所求的三角形.其中AB=$\sqrt{5}$a、AC=2$\sqrt{2}$a、BC=$\sqrt{17}$a.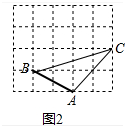
(3)如图3所示:△ABC就是所求的三角形.其中AB=$\sqrt{{m}^{2}+16{n}^{2}}$、BC=$\sqrt{9{m}^{2}+4{n}^{2}}$、AC=2$\sqrt{{m}^{2}+{n}^{2}}$.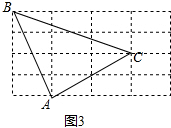
点评 本题考查勾股定理、作图设计应用等知识,解题的关键是灵活应用勾股定理解决问题,体现了数形结合的思想,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计)一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校共用10分钟.下列说法:
小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计)一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校共用10分钟.下列说法:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com