
分析 将两个方程分别因式分解可得(x-y+1)(x-y-1)=0且(x+y+2)(x+y-5)=0,继而可得.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-2xy+{y}^{2}=1}&{①}\\{(x+y)^{2}-3(x+y)-10=0}&{②}\end{array}\right.$,
由①可得(x-y)2-1=0,
(x-y+1)(x-y-1)=0,
∴x-y+1=0或x-y-1=0,
由②可得(x+y+2)(x+y-5)=0,
∴x+y+2=0或x+y-5=0,
∴原方程组可化为$\left\{\begin{array}{l}{x-y+1=0}\\{x+y+2=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+1=0}\\{x+y-5=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y-1=0}\\{x+y+2=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y-1=0}\\{x+y-5=0}\end{array}\right.$来解,
故答案为:$\left\{\begin{array}{l}{x-y+1=0}\\{x+y+2=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+1=0}\\{x+y-5=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y-1=0}\\{x+y+2=0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y-1=0}\\{x+y-5=0}\end{array}\right.$.
点评 本题主要考查解高次方程的能力,解二元二次方程组的基本思想是“转化”,这种转化包含“消元”和“降次”将二元转化为一元是消元,将二次转化为一次是降次,这是转化的基本方法.因此,掌握好消元和降次的一些方法和技巧是解二元二次方程组的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:填空题
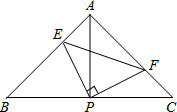 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
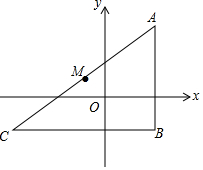 如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )
如图,在Rt△ABC中,∠B=90°,AB垂直于x轴,M为AC的中点,若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为( )| A. | (3,-4) | B. | (3,-3) | C. | (3,-2) | D. | (3,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=x-$\sqrt{2}$与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,已知AO=AC.
如图,直线y=x-$\sqrt{2}$与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,已知AO=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com