已知直线y=-2x-4与x轴、y轴分别交于A、B两点,点C在x轴负半轴上,AC=2.
(1)点P在直线y=-2x-4上,△PAC是以AC为底的等腰三角形,
①求点P的坐标和直线CP的解析式;
②请利用以上的一次函数解析式,求不等式-x-2>x+4的解集.
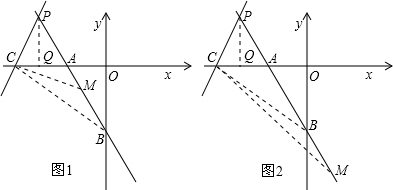
(2)若点M(x,y)是射线AB上的一个动点,在点M的运动过程中,试写出△BCM的面积S与x的函数关系式,并画出函数图象.
解:(1)∵一次函数y=-2x-4与x、y轴交于A、B两点,
∴令x=0求出y=-4;令y=0求出x=-2,
∴A(-2,0),B(0,-4),
∵AC=2,点C在x轴的负半轴上,
∴C(-4,0),
过P作PQ⊥x轴,
∵△PAC是以AC为底的等腰三角形,
∴Q为AC的中点,即P横坐标为-3,
将x=-3代入y=-2x-4中得:y=6-4=2,
∴P(-3,2),
设直线PC解析式为y=kx+b,
将P与C坐标代入得:

,
解得:
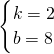
,
∴直线PC的解析式为y=2x+8;
(2)由-x-2>x+4,可得-2x-4>2x+8,
令y
1=-2x-4,y
2=2x+8,
当y
1>y
2时,由图象可知x<-3,
故不等式-x-2>x+4的解集是x<-3;
(3)当点M在线段AB上时,如图1所示,
S=S
△ABC-S
△ACM=

×2×4-

×2×(2x+4)=

×2×(4-2x-4)=-2x(-2≤x<0);
当点M在线段AB的延长线上时,如图2所示,S=S
△ACM-S
△ABC=2x(x>0),
综上,S=
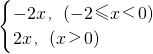
,
作出图象,如图所示:

分析:(1)①对于一次函数y=-2x-4,分别令x与y为0求出对应y与x的值,确定出A与B的坐标,再由AC为2,且C在x轴的负半轴上求出C的坐标,三角形PAC是以AC为底边的等腰三角形得到P的横坐标为-3,代入直线方程求出纵坐标,即可确定出P的坐标,设直线CP解析式为y=kx+b,将P与C坐标代入求出k与b的值,即可确定出直线CP的解析式;
②将所求不等式变形,利用图象即可求出解集;
(2)分两种情况考虑:当M在线段AB上时,三角形BCM的面积=三角形ABC面积-三角形ACM的面积,表示出S与X关系式即可;当M在线段AB延长线上时,三角形BCM的面积-三角形ACM面积-三角形ABC面积,表示出S与x关系式即可,并画出相应的图象,如图所示.
点评:此题考查了一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,待定系数法求函数解析式,坐标与图形性质,利用了分类讨论及数形结合的思想,是一道中档题.


 ,
,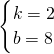 ,
, ×2×4-
×2×4- ×2×(2x+4)=
×2×(2x+4)= ×2×(4-2x-4)=-2x(-2≤x<0);
×2×(4-2x-4)=-2x(-2≤x<0); 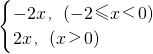 ,
,


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案