
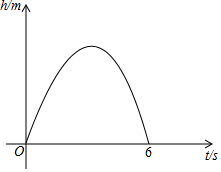
 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).分析 (1)首先理解题意,先把实际问题转化成数学问题后,知道解此题就是求出h=30t-5t2的顶点坐标即可.
(2)相当于求h=25时,t的值,即可.
解答 解:(1)∵h=-5t2+30t=-5(t2-6t+9)+45=-5(t-3)2+45,
∵a=-5<0,
∴图象的开口向下,有最大值,
当t=3时,h最大值=45,
∴小球运动的时间是3s时,小球最高,小球运动中的最大高度是45m.
(2)由题意h=25,
∴-5t2+30t=25,
∴t2-6t+5=0,
∴t=1或5,
∵小球下落过程中,接住小球,
∴t=5s.
∴这时小球从抛出到小明接住小球用了5s.
点评 本题考查了二次函数的应用,解此题的关键是熟练掌握配方法确定函数顶点坐标,也可以用顶点坐标公式求顶点坐标,属于中考基础题,常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
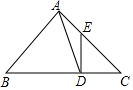 在△ABC中,∠BAC=90°,∠B=45°,D为BC上一点,BD=AB,DE⊥BC,交AC于点E.
在△ABC中,∠BAC=90°,∠B=45°,D为BC上一点,BD=AB,DE⊥BC,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com