
分析 (1)根据题意依次列算式,再提取$\frac{1}{3}$,即可得出结果;
(2)两个连续的自然数的积等于这两个数与后面的数相乘减去这两个数与前面的数相乘的三分之一,按此规律代入计算即可;
(3)1×2+2×3+3×4根据(1)中的规律进行计算,3×4×5+…+6×7×8等,类比1×2、2×3等得出结论:3×4×5=$\frac{1}{4}$(3×4×5×6-2×3×4×5),4×5×6=$\frac{1}{4}$(4×5×6×7-3×4×5×6)…代入计算即可;
(4)类比(3)中的结论进行计算.
解答 解:(1)∵1×2=$\frac{1}{3}$(1×2×3-0×1×2),2×3=$\frac{1}{3}$(2×3×4-1×2×3),3×4=$\frac{1}{3}$(3×4×5-2×3×4)
4×5=$\frac{1}{3}$(4×5×6-3×4×5),5×6=$\frac{1}{3}$(5×6×7-4×5×6),6×7=$\frac{1}{3}$(6×7×8-5×6×7)
由以上六个等式相加,可得4×5+5×6+6×7=$\frac{1}{3}$×(6×7×8-3×4×5)=92
∴1×2+2×3+3×4+…+6×7
=$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+…+$\frac{1}{3}$(6×7×8-5×6×7),
=$\frac{1}{3}$×6×7×8
=112;
(2)1×2+2×3+3×4+…+n×(n+1),
=$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+…+$\frac{1}{3}$[n(n+1)(n+2)-n(n-1)(n+1)],
=$\frac{1}{3}$n(n+1)(n+2);
(3)∵3×4×5=$\frac{1}{4}$(3×4×5×6-2×3×4×5),4×5×6=$\frac{1}{4}$(4×5×6×7-3×4×5×6),
5×6×7=$\frac{1}{4}$(5×6×7×8-4×5×6×7),6×7×8=$\frac{1}{4}$(6×7×8×9-5×6×7×8),
又∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20,
∴1×2+2×3+3×4+3×4×5+…+6×7×8,
=20+$\frac{1}{4}$(3×4×5×6-2×3×4×5)+$\frac{1}{4}$(4×5×6×7-3×4×5×6)+$\frac{1}{4}$(5×6×7×8-4×5×6×7)+$\frac{1}{4}$(6×7×8×9-5×6×7×8),
=20+$\frac{1}{4}$×6×7×8×9-$\frac{1}{4}$×2×3×4×5,
=20+756-30,
=746;
(4)1×2+2×3+3×4+3×4×5+…+n(n+1)×(n+2),
=20+$\frac{1}{4}$n(n+1)(n+2)(n+3)-$\frac{1}{4}$×2×3×4×5,
=$\frac{1}{4}$n(n+1)(n+2)(n+3)-10.
故答案为:(1)112;(2)$\frac{1}{3}$n(n+1)(n+2);(3)746;(4)$\frac{1}{4}$n(n+1)×(n+2)(n+3)-10.
点评 本题考查了数字类的变化规律,比较复杂,要认真观察,仔细思考;根据类比和归纳的思想进行推理,从而得出结论,并利用后面的数进行验证.


科目:初中数学 来源: 题型:解答题
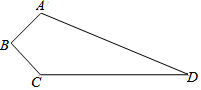 如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?
如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(3,0)、(3,6),若经过O、A两点的抛物线y=ax2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和是$\frac{9}{2}$.
如图:在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(3,0)、(3,6),若经过O、A两点的抛物线y=ax2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和是$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com