练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知x2-2xy-15y2=0，求$\frac{x+y}{x-y}$．

    分析 根据x2-2xy-15y2=0利用因式分解可得出x=-3y或x=5y，将其代入分式中即可得出结论．

    解答 解：∵x2-2xy-15y2=（x+3y）（x-5y）=0，
    ∴x=-3y或x=5y．
    当x=-3y时，$\frac{x+y}{x-y}$=$\frac{-3y+y}{-3y-y}$=$\frac{1}{2}$；
    当x=5y时，$\frac{x+y}{x-y}$=$\frac{5y+y}{5y-y}$=$\frac{3}{2}$．

    点评 本题考查了利用十字相乘法分解因式，利用十字相乘法将多项式分解成（x+3y）（x-5y）=0是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届江苏省无锡市九年级3月月考数学试卷（解析版） 题型：判断题

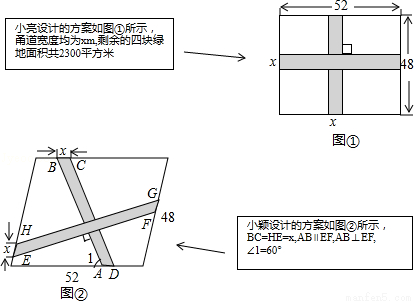
    要在一块长52m，宽48m的矩形绿地上，修建同样宽的两条互相垂直的甬路．下面分别是小亮和小颖的设计方案．

    （1）求小亮设计方案中甬路的宽度x；

    （2）求小颖设计方案中四块绿地的总面积（友情提示：小颖设计方案中的与小亮设计方案中的取值相同）

    查看答案和解析>>

    科目：初中数学 来源：2017届辽宁省丹东市九年级第一次模拟考试数学试卷（解析版） 题型：填空题

    不等式组的解集为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．已知a，b是实数，设A=$\left\{\begin{array}{l}a，（a≤b）\\ b，（a＞b）\end{array}$，B=$\left\{\begin{array}{l}b，（a≤b）\\ a，（a＞b）\end{array}$，C=$\frac{a+b}{2}$，则下列各式中，错误的是（　　）
    A．A≤CB．B≥CC．A+B=2CD．A2+B2=C2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．当x=-1或3，代数式x2-2的值与2x+1的值相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．给出一种运算：对于函数y=xn，规定y'=nxn-1．例如：若函数y=x4，则有y'=4x3．已知函数y=x3，则方程y'=12的解是x1=2，x2=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，为了确定一条河的宽度，测量人员在对岸岸边P点处观察到一根柱子，再在他们所在的这一侧岸上选点A和点B，使得B，A，P在同一条直线上，且与河岸垂直，随后确定点C，点D，使BC⊥BP，AD⊥BP，由观测可以确定CP与AD的交点D．他们测得AB=45m，BC=90m，AD=60m，从而确定河宽，他们测量的河宽为90 m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．将一副常规的直角三角尺（分别含30°和45°角）按如图方式放置，则图中∠AOB的度数为（　　）
    A．75°B．95°C．105°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连结BE，
    ①求证：△ACD≌△BCE；
    ②求∠AEB的度数．
    （2）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请求∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案