
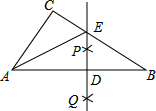
 如图,点C在线段BD上,AB⊥BD,PD⊥BD,∠B=∠D=90°,AB=3,BC=6,CD=2,则当DE=1或4时,△ABC与△CDE相似.
如图,点C在线段BD上,AB⊥BD,PD⊥BD,∠B=∠D=90°,AB=3,BC=6,CD=2,则当DE=1或4时,△ABC与△CDE相似. 分析 根据已知分两种情况△ABC∽△CDE或△ABC∽△EDC来进行分析,根据相似三角形的性质确定DE的长.
解答 解:①△ABC∽△CDE,则
$\frac{AB}{CD}$=$\frac{BC}{DE}$,即$\frac{3}{2}$=$\frac{6}{DE}$,
解得DE=4;
②△ABC∽△EDC,则
$\frac{AB}{ED}$=$\frac{BC}{DC}$,即$\frac{3}{DE}$=$\frac{6}{2}$,
解得DE=1.
故答案为:1或4.
点评 此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com