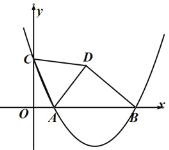
【题目】如图，在平面直角坐标系中，点C是y轴正半轴上的一个动点，抛物线y＝ax2－6ax+5a（a是常数，且a＞0）过点C，与x轴交于点A、B，点A在点B的左边．连接AC，以AC为边作等边三角形ACD，点D与点O在直线AC两侧，连接BD，则BD的最小值是_________．
【答案】3
【解析】
由抛物线的性质先求
三点坐标，过点D作DE⊥AC于点E，过点D作x轴的垂线于点H，过点E作EF∥x轴交y轴于点F交DH于点G，利用等边三角形与相似三角形的性质求解
的坐标，利用两点间距离公式建立
与
之间的函数关系式，利用函数性质求
的最小值．
解：
如图，过点D作DE⊥AC于点E，过点D作x轴的垂线于点H，过点E作EF∥x轴交y轴于点F交DH于点G，
∵△ACD为等边三角形，则点E为AC的中点，
则点E（ 
），AE=CE=
ED，
∵∠CEF+∠FCE=90°，∠CEF+∠DEG=90°，
∴∠DEG=∠ECF，
∴△CFE∽△EGD，
∴ 
为
中点，
轴，
解得：GE=
，DG=
故点D（ 
），
故当
时，的最小值
的最小值为
（负根舍去）
故答案为：
考前必练系列答案科目：初中数学 来源： 题型：
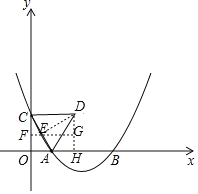
【题目】如图1，在
中，
，
．
问题情境1：（1）
与
的数量关系为_______；
问题情境2：（2）如图2，若
，且
，则
与
的数量关系是什么．请说明理由；
拓展延伸：（3）将图2中的
绕点
顺时针旋转角度
（
），在旋转过程中，当
，
，
三点在同一条直线上时，请直接写出
，，
之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某幼儿园举行用火柴棒摆“金鱼”比赛，如图所示，请仔细观察并找出规律，解答下列问题：
(1)按照此规律，摆第n个图时，需用火柴棒的根数是多少？
(2)求摆第50个图时所需用的火柴棒的根数；
(3)按此规律用1202根火柴棒摆出第n个图形，求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
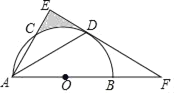
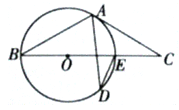
【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为
的中点，作DE⊥AC，交AB的延长线于点F，连接DA．
（1）求证：EF为半圆O的切线；
（2）若DA＝DF＝6
，求阴影区域的面积．（结果保留根号和π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C
（I）若∠ADE=25°，求∠C的度数
（II）若AB=AC，求∠D的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图平面直角坐标系，已知二次函数
（m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．
（1）点B的坐标为 ，点D的坐标为 ；（用含有m的代数式表示）
（2）连接CD，BC．
①若
，求二次函数的表达式；
②若把ABC沿着直线BC翻折，点A恰好在直线CD上，求二次函数的表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解高邮市“新冠肺炎”疫情防控期间九年级学生线上学习情况，通过问卷网就“你对自己线上学习的效果评价”进行了问卷调查，从中随机抽取了部分样卷进行统计，绘制了如下的统计图
根据统计图信息，解答下列问题：
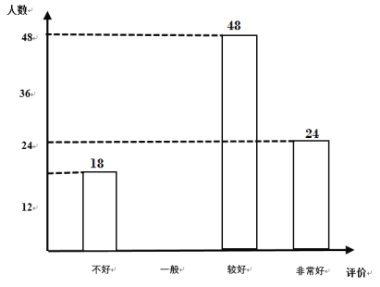
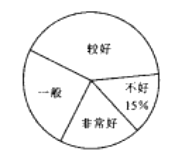
（1）本次调查的样本容量为 ；
（2）请补全条形统计图；
（3）扇形统计图中“较好”对应的扇形圆心角的度数为 
；
（4）若全市九年级线上学习人数有
人，请估计对线上学习评价“非常好”的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，对于任意两点P1(x1，y1)与P2(x2，y2)的“非常距离”，给出如下定义：
若|x1x2|≥|y1y2|，则点P1与点P2的“非常距离”为|x1x2|；
若|x1x2||y1y2|，则点P1与点P2的“非常距离”为|y1y2|.
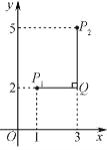
例如：点P1(1，2)，点P2(3，5)，因为|13||25|，所以点P1与点P2的“非常距离”为|25|3，也就是图中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点）.
（1）已知点A(0,1)，
①在B(
,0)，C(2,1)，D(1,2)，E(0,
)四个点中，与点A的“非常距离”为的点是；
②点F为x轴上一动点，直接写出点A与点F的“非常距离”的最小值；
（2）已知点M是直线y2x6上的一个动点，
①点G的坐标是（0，2），求点M与点G的“非常距离”的最小值及相应的点M的坐标；
①点N是以点（4，0）为圆心，
为半径的圆上的一个动点，直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在B左边），与y轴交于点C．
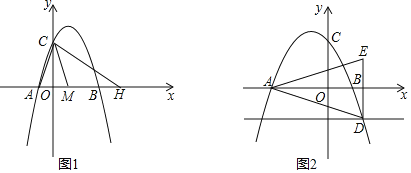
（1）如图1，已知A(﹣1，0)，B(3，0)．
①直接写出抛物线的解析式；
②点H在x轴上，M(1，0)，连接AC、MC、HC，若CM平分∠ACH，求H的坐标；
（2）如图2，直线y＝﹣1与抛物线y＝﹣x2+bx+c交于抛物线对称轴右侧的点为点D，点E与点D关于x轴对称．试判断直线DB与直线AE的位置关系，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com