
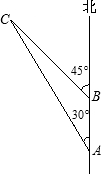
 如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?(
如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?(| 3 |
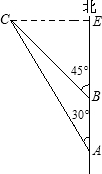 解:轮船不会触礁. (2分)
解:轮船不会触礁. (2分)| CE |
| AE |
| x |
| x+1200 |
| 1 | ||
|
| 3 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省建水三合中学八年级上学期期中考试数学试卷(带解析) 题型:解答题
(本题满分6分)如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,求从B到灯塔C的距离。
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷数学卷 题型:解答题
(本小题满分8分)
如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,求从B到灯塔C的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com