Question

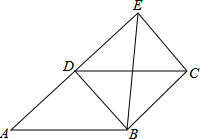
6．如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（　　）

• A． AB=BE
• B． BE⊥DC
• C． ∠ADB=90°
• D． CE⊥DE

Answer 1

分析 先证明四边形BCDE为平行四边形，再根据矩形的判定进行解答．

解答 解：∵四边形ABCD为平行四边形，
∴AD∥BC，AD=BC，
又∵AD=DE，
∴DE∥BC，且DE=BC，
∴四边形BCED为平行四边形，
A、∵AB=BE，DE=AD，∴BD⊥AE，∴?DBCE为矩形，故本选项错误；
B、∵对角线互相垂直的平行四边形为菱形，不一定为矩形，故本选项正确；
C、∵∠ADB=90°，∴∠EDB=90°，∴?DBCE为矩形，故本选项错误；
D、∵CE⊥DE，∴∠CED=90°，∴?DBCE为矩形，故本选项错误．
故选B．

点评 本题考查了平行四边形的判定和性质、矩形的判定，首先判定四边形BCDE为平行四边形是解题的关键．