
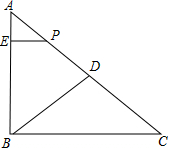
 ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬AC=10cm£¬BC=8cm£¬µćDŹĒĻ߶ĪACµÄÖŠµć£¬¶ÆµćP“ÓµćA³ö·¢£¬ŃŲA-D-B-CĻņÖÕµćCŌĖ¶Æ£¬ĖŁ¶ČĪŖ5cm/s£¬µ±µćP²»ÓėµćA£¬BÖŲŗĻŹ±£¬×÷PE”ĶAB½»Ļ߶ĪABÓŚµćE£¬ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖt£Øs£©£¬”÷APEµÄĆ껿ĪŖS£Øcm2£©£®
ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬AC=10cm£¬BC=8cm£¬µćDŹĒĻ߶ĪACµÄÖŠµć£¬¶ÆµćP“ÓµćA³ö·¢£¬ŃŲA-D-B-CĻņÖÕµćCŌĖ¶Æ£¬ĖŁ¶ČĪŖ5cm/s£¬µ±µćP²»ÓėµćA£¬BÖŲŗĻŹ±£¬×÷PE”ĶAB½»Ļ߶ĪABÓŚµćE£¬ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖt£Øs£©£¬”÷APEµÄĆ껿ĪŖS£Øcm2£©£®·ÖĪö £Ø1£©ŌŚRt”÷ABCÖŠ£¬øł¾Ż¹“¹É¶ØĄķ¼“æɽā¾öĪŹĢā£®
£Ø2£©Ö»ŅŖÖ¤Ć÷”÷PBE”×”÷CAB£¬æɵĆ$\frac{PE}{PB}$=$\frac{BC}{AC}$£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
£Ø3£©·ÖĮ½ÖÖĒéŠĪĢÖĀŪ¢Łµ±0£¼t”Ü1Ź±£®¢Śµ±1£¼t£¼2Ź±£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½Ēó³öAE”¢PE¼“æɽā¾öĪŹĢā£®
£Ø4£©Ēó³öĮ½øöĢŲŹāµćµÄŹ±¼ä¢ŁČēĶ¼1ÖŠ£¬µ±µćE¹ŲÓŚAPµÄ¶Ō³ĘµćE”äŌŚĻ߶ĪACÉĻŹ±£®ČēĶ¼2ÖŠ£¬µ±µćPŌŚBCÉĻ£¬µćE¹ŲÓŚAPµÄ¶Ō³ĘµćE”äŌŚĻ߶ĪACÉĻŹ±£®¼“æɽā¾öĪŹĢā£®
½ā“š ½ā£ŗ£Ø1£©”ßŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬AC=10cm£¬BC=8cm£¬
”ąAB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6£¬
¼“ABµÄ³¤ĪŖ6£»
£Ø2£©”ßPE”ĶAB£¬BC”ĶAB£¬
”ąPE”ĪBC£¬”ĻABC=”ĻBEP=90”ć£¬
”ą”ĻEPB=”ĻPBC£¬
”ßµćDĪŖACÖŠµć£¬
”ąBD=CD=$\frac{1}{2}$AC£¬
”ą”ĻDBC=”ĻDCB£¬
”ą”ĻEPB=”ĻDCB£¬
”ą”÷PBE”×”÷CAB£¬
”ą$\frac{PE}{PB}$=$\frac{BC}{AC}$£¬
”ą$\frac{PE}{10-5t}$=$\frac{8}{10}$£¬
”ßBP=10-5t£¬
”ąPE=8-4t£®
£Ø3£©µ±0£¼t”Ü1Ź±
AE=5t”Į$\frac{3}{5}$=3t£¬PE=5t”Į$\frac{4}{5}$=4t£¬
S=$\frac{1}{2}$•PE•AE=$\frac{1}{2}$•4t•3t=6t2£¬
”ąS=6t2£®
µ±1£¼t£¼2Ź±£¬
AE=6-£Ø10-5t£©$\frac{3}{5}$=3t£¬PE=£Ø10-5t£©”Į$\frac{4}{5}$=8-4t£¬
S=$\frac{1}{2}$•PE•AE=$\frac{1}{2}$•3t•£Ø8-4t£©=-6t2+12t£®
”ąS=-6t2+12t£¬
×ŪÉĻĖłŹö£¬S=$\left\{\begin{array}{l}{6{t}^{2}}&{£Ø0£¼t”Ü1£©}\\{-6{t}^{2}+12t}&{£Ø1£¼t£¼2£©}\end{array}\right.$£®
£Ø4£©ČēĶ¼1ÖŠ£¬µ±µćE¹ŲÓŚAPµÄ¶Ō³ĘµćE”äŌŚĻ߶ĪACÉĻŹ±£®×÷PE”ä”ĶACÓŚE”䣬ŌņPE=PE”ä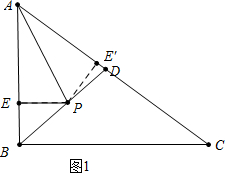
”ß$\frac{{S}_{”÷APB}}{{S}_{”÷APD}}$=$\frac{\frac{1}{2}•AB•PE}{\frac{1}{2}•AD•PE”ä}$=$\frac{PB}{PD}$£¬
”ą$\frac{AB}{AD}$=$\frac{PB}{PD}$£¬
”ą$\frac{6}{5}$=$\frac{5-PD}{PD}$£¬
”ąPD=$\frac{25}{11}$£¬
”ąµćPŌĖ¶ÆµÄŹ±¼ä=£Ø5+$\frac{25}{11}$£©”Ā5=$\frac{16}{11}$s£¬
¹Ū²ģĶ¼ĻóæÉÖŖµ±$\frac{16}{11}$£¼t£¼2Ź±£¬µ±µćE”äĀäŌŚ”÷ABCµÄÄŚ²æ£®
ČēĶ¼2ÖŠ£¬µ±µćPŌŚBCÉĻ£¬µćE¹ŲÓŚAPµÄ¶Ō³ĘµćE”äŌŚĻ߶ĪACÉĻŹ±£®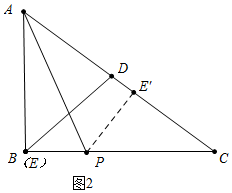
Ķ¬ĄķæɵĆ$\frac{AB}{AC}$=$\frac{PB}{PC}$£¬
”ą$\frac{6}{10}$=$\frac{PB}{8-PB}$£¬
”ąPB=3£¬
”ą”ąµćPŌĖ¶ÆµÄŹ±¼ä=£Ø5+5+3£©”Ā5=$\frac{13}{5}$s
¹Ū²ģĶ¼ĻóæÉÖŖµ±2£¼t£¼$\frac{13}{5}$Ź±£¬µ±µćE”äĀäŌŚ”÷ABCµÄÄŚ²æ£®
×ŪÉĻĖłŹö£¬µ±$\frac{16}{11}$£¼t£¼2»ņ2£¼t£¼$\frac{13}{5}$Ź±£¬µ±µćE”äĀäŌŚ”÷ABCµÄÄŚ²æ£®
µćĘĄ ±¾Ģāæ¼²éČż½ĒŠĪ×ŪŗĻĢā”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¹“¹É¶ØĄķ£®½ĒĘ½·ÖĻߵĊŌÖŹ¶ØĄķµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŹī¼Ł×÷ŅµŠĀ½®ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŹī¼Ł×÷ŅµŠĀ½®ČĖĆń³ö°ęÉēĻµĮŠ“š°ø Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Óµ¼ÓėĮ·Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø
Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Óµ¼ÓėĮ·Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø Š”ѧŹī¼Ł×÷Ņµ¶«ÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø
Š”ѧŹī¼Ł×÷Ņµ¶«ÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø ½ņĒŽĢÓżŹī¼Ł°ĪøßĻĪ½Ó¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
½ņĒŽĢÓżŹī¼Ł°ĪøßĻĪ½Ó¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø ²Ø²ØŠÜŹī¼Ł×÷Ņµ½Ī÷ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
²Ø²ØŠÜŹī¼Ł×÷Ņµ½Ī÷ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
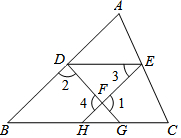 ČēĶ¼£¬ŅŃÖŖ”Ļ1+”Ļ2©180”ć£¬”Ļ3©”ĻB£¬ŌņDE”ĪBC£¬ĻĀĆęŹĒĶõ»ŖĶ¬Ń§µÄĶʵ¼¹ż³Ģ©oĒėÄć°ļĖūŌŚĄØŗÅÄŚĢīÉĻĶʵ¼ŅĄ¾Ż»ņÄŚČŻ£®
ČēĶ¼£¬ŅŃÖŖ”Ļ1+”Ļ2©180”ć£¬”Ļ3©”ĻB£¬ŌņDE”ĪBC£¬ĻĀĆęŹĒĶõ»ŖĶ¬Ń§µÄĶʵ¼¹ż³Ģ©oĒėÄć°ļĖūŌŚĄØŗÅÄŚĢīÉĻĶʵ¼ŅĄ¾Ż»ņÄŚČŻ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® | 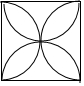 | C£® | 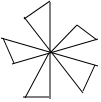 | D£® | 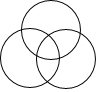 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | m£¾1 | B£® | m£¼$\frac{1}{2}$ | C£® | $\frac{1}{2}$£¼m£¼1 | D£® | m£¼$\frac{1}{2}$»ņm£¾1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
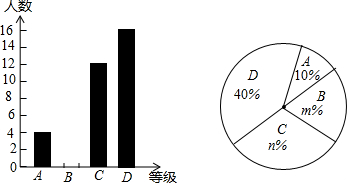
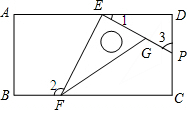 ČēĶ¼£¬Ņ»øöŗ¬ÓŠ30”ć½ĒµÄÖ±½ĒČż½Ē°åµÄĮ½øö¶„µćE”¢F·ÅŌŚŅ»øö³¤·½ŠĪµÄ¶Ō±ßÉĻ£¬µćEĪŖÖ±½Ē¶„µć£¬”ĻEFG=30”ć£¬ŃÓ³¤EG½»CDÓŚµćP£¬Čē¹ū”Ļ3=65”ć£¬ÄĒĆ“”Ļ2µÄ¶ČŹżŹĒ£Ø””””£©
ČēĶ¼£¬Ņ»øöŗ¬ÓŠ30”ć½ĒµÄÖ±½ĒČż½Ē°åµÄĮ½øö¶„µćE”¢F·ÅŌŚŅ»øö³¤·½ŠĪµÄ¶Ō±ßÉĻ£¬µćEĪŖÖ±½Ē¶„µć£¬”ĻEFG=30”ć£¬ŃÓ³¤EG½»CDÓŚµćP£¬Čē¹ū”Ļ3=65”ć£¬ÄĒĆ“”Ļ2µÄ¶ČŹżŹĒ£Ø””””£©| A£® | 100”ć | B£® | 105”ć | C£® | 115”ć | D£® | 120”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | £Øm-2£©£Øm+2£©=m2-2 | B£® | £Øx-6£©£Øx+6£©=x2+36 | C£® | £Øx-y£©£Øx+y£©=x2-y2 | D£® | £Øx+y£©£Øx+y£©=x2+y2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com