
【题目】解下列方程
(1)(x﹣8)(x﹣1)=﹣12;
(2)3(x﹣5)2=2(5﹣x).
(3)y2-7y+6=0;
(4)2x2-4x-3=0;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ; (4)
; (4)![]() .
.
【解析】
(1)把方程左边化简,移项,合并整理后,利用十字相乘法求解即可;
(2)先移项,变形,再提公因式解答即可;
(3)利用十字相乘法求解即可;
(4)利用配方法求解即可.
解:(1)(x﹣8)(x﹣1)=﹣12,
x-x-8x+12=0,
x-9x+20=0,
(x-4)(x-5)=0 ,
则x-4=0或x-5=0,
解得:![]() ;
;
(2)3(x﹣5)2=2(5﹣x),
3(x-5)+2(x-5)=0,
(x-5)![]() =0,
=0,
(x-5)(3x-13)=0,
则x-5=0或3x-13=0,
解得: ![]() ;
;
(3)y2-7y+6=0,
(y-6)(y-1)=0,
则y-6=0或y-1=0,
解得:![]() ;
;
(4)2x2-4x-3=0,
2x-4x-3=2(x-1)-5=0,
(x-1)=![]() ,
,
则x-1=![]() 或x-1= -
或x-1= -![]() ;
;
解得: ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
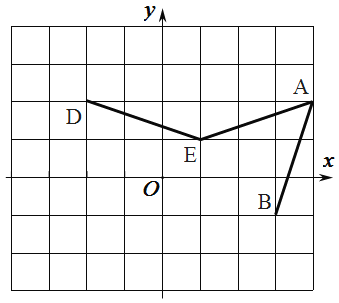
【题目】如图,在边长为1的正方形网格中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得
得![]() (点
(点![]() 与点
与点![]() 对应).
对应).
(1)直接写出![]() 的值:
的值:![]() ;
;
(2)用无刻度直尺作出点![]() 并直接写出
并直接写出![]() 的坐标(保留作图痕迹,不写作法);
的坐标(保留作图痕迹,不写作法);
(3)若格点![]() 在
在![]() 的角平分线上,这样的格点
的角平分线上,这样的格点![]() (不包括点
(不包括点![]() 有) 个(直接写出答案)
有) 个(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围.
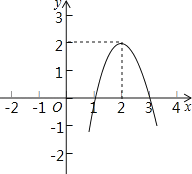
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P在△ABC内,且满足∠APB=∠APC(如下图),∠APB+∠BAC=180°,
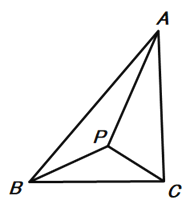
(1)求证:△PAB∽△PCA:
(2)如下图,如果∠APB=120°,∠ABC=90°求![]() 的值;
的值;
(3)如图,当∠BAC=45°,△ABC为等腰三角形时,求tan∠PBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共10只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
(2)试估算口袋中黑、白两种颜色的球各有多少只?
(3)请画树状图或列表计算:从中一次摸两只球,这两只球颜色不同的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com