
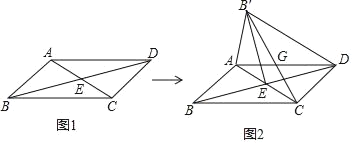
【题目】ABCD中,对角线AC与BD相交于点E,将△ABC沿AC所在直线翻折至△AB′C,若点B的落点记为B′,连接B′D、B′C,其中B′C与AD相交于点G.
①△AGC是等腰三角形;②△B′ED是等腰三角形;
③△B′GD是等腰三角形;④AC∥B′D;
⑤若∠AEB=45°,BD=2,则DB′的长为![]() ;
;
其中正确的有( )个.

A. 2B. 3C. 4D. 5
【答案】D
【解析】
利用平行四边形的性质、翻折不变性一一判断即可解决问题;
解:∵四边形ABCD是平行四边形,
∴BE=DE,AD∥BC,AD=BC,
∴∠GAC=∠ACB,
由翻折可知:BE=EB′=DE,∠ACB=∠ACG,CB=CB′,
∴∠GAC=∠ACG,
∴△AGC,△B′ED是等腰三角形,故①②正确,
∵AB′=AB=DC,CB′=AD,DB′=B′D,
∴△ADB′≌△CB′D,
∴∠ADB′=∠CB′D,
∴GD=GB′,
∴△B′GD是等腰三角形,故③正确,
∵∠GAC=∠GCA,∠AGC=∠DGB′,
∴∠GAC=∠GDB′,
∴AC∥DB′,故④正确.
∵∠AEB=45°,BD=2,
∴∠BEB′=∠DEB′=90°,
∵DE=EB′=1,
∴DB′=![]() ,故⑤正确.
,故⑤正确.
故选:D.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.
(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .
(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)如图2,连接BE,若AB=2![]() ,BE=2
,BE=2![]() ,求AP的长.
,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
因式分解:![]() .
.
解:将“![]() ”看成整体,令
”看成整体,令![]() ,则原式
,则原式![]() .
.
再将“![]() ”还原,原式
”还原,原式![]() .
.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
(问题解决)
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)证明:若![]() 为正整数,则代数式
为正整数,则代数式![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二元一次方程组![]() 的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰)
的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 方向运动再过点
方向运动再过点![]() 沿
沿![]() 方向运动,到点
方向运动,到点![]() 停止运动,点
停止运动,点![]() 以同样的速度从点
以同样的速度从点![]() 出发沿着
出发沿着![]() 方向运动,到点
方向运动,到点![]() 停止运动,设点
停止运动,设点![]() 运动的路程为
运动的路程为![]() .
.
(1)当![]() 时,线段
时,线段![]() 的长是 ;
的长是 ;
(2)当点![]() 在线段
在线段![]() 上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
上运动时,图中阴影部分的面积会发生改变吗?请你作出判断并说明理由.
(3)在点![]() 的运动过程中,是否存在某一时刻,使得
的运动过程中,是否存在某一时刻,使得![]() ?若存在,求出点
?若存在,求出点![]() 的运动路程,若不存在,请说明理由.
的运动路程,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com