
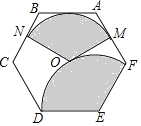
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
科目:初中数学 来源: 题型:
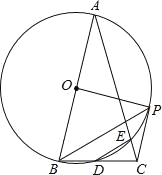
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
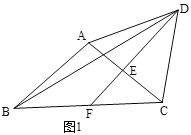
【题目】在△ABC中,AB=AC,在△ABC的外部作等边三角形△ACD,E为AC的中点,连接DE并延长交BC于点F,连接BD.
(1)如图1,若∠BAC=100°,则∠ABD的度数为_____,∠BDF的度数为______;
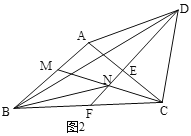
(2)如图2,∠ACB的平分线交AB于点M,交EF于点N,连接BN,若BN=DN,∠ACB=![]() .
.
(I)用![]() 表示∠BAD;
表示∠BAD;
(II)①求证:∠ABN=30°;
②直接写出![]() 的度数以及△BMN的形状.
的度数以及△BMN的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
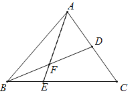
【题目】如图,在![]() 中,
中,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 交于点
交于点![]() ,
,![]() .若
.若![]() 的面积为18,给出下列命题:①
的面积为18,给出下列命题:①![]() 的面积为16;②
的面积为16;②![]() 的面积和四边形
的面积和四边形![]() 的面积相等;③点
的面积相等;③点![]() 是
是![]() 的中点;④四边形
的中点;④四边形![]() 的面积为
的面积为![]() ;其中,正确的结论有_____________.
;其中,正确的结论有_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,矩形
中,矩形![]() 如图放置,动点
如图放置,动点![]() 从
从![]() 出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成
出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成![]() 度角(反弹后仍在矩形内作直线运动),当点
度角(反弹后仍在矩形内作直线运动),当点![]() 第
第![]() 次碰到矩形的边时,点
次碰到矩形的边时,点![]() 的坐标为
的坐标为![]() ;当点
;当点![]() 第
第![]() 次碰到矩形的边时,点
次碰到矩形的边时,点![]() 的坐标为 __________.
的坐标为 __________.

查看答案和解析>>
科目:初中数学 来源: 题型:
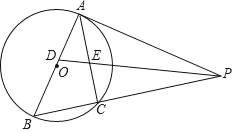
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
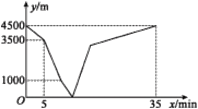
【题目】小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发5分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟.两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
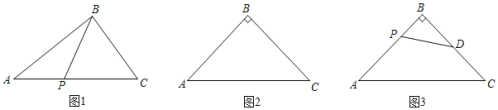
【题目】(1)问题探究
①如图1,在直角△ABC中,∠ABC=90°,AC=5,BC=3,P是AC边上一点,连接BP,则BP的最小值为 .
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a,求边AB的长度(用含a的代数式表示).
(2)问题解决
如图3,在等腰直角△ABC中,∠ABC=90°,AC=2![]() ,D是边BC的中点,若P是AB边上一点,试求:PD+
,D是边BC的中点,若P是AB边上一点,试求:PD+![]() AP的最小值.
AP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.

(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△ONC的面积是△OAC面积的![]() 时,求出这时点N的坐标.
时,求出这时点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com