Question

19．在△ABC中，AB=20，AC=13，高AD=12，求△ABC的面积．

Answer 1

分析 根据勾股定理分别求出BD、CD的长，根据△ABC是锐角或钝角三角形进行计算即可．

解答 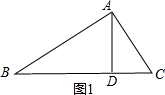解：如图1，∵AD⊥BC，
∴∠ADB=90°，
又∵AB=20，AD=12，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=16，
∴∠ADC=90°，又AC=13，AD=12，
∴CD=5，
∴BC=BD+CD=21，
∴△ABC的面积=$\frac{1}{2}$×21×12=126；
如图2，BC=BD-CD=11，
∴△ABC的面积=$\frac{1}{2}$×11×12=66．

点评 本题考查的是勾股定理的应用，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a²+b²=c²．