
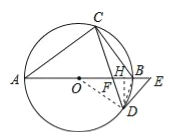
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)详见解析;(2)5.
【解析】
试题(1)连接OD,由AB是⊙O的直径可得∠ACB=90°,所以∠A+∠ABC=90°,即可证得∠BOD=∠A,从而推出∠ODE=90°,即可得到结论;(2)连接BD,过D作DH⊥BF于H,由弦切角定理得到∠BDE=∠BCD,推出△ACF与△FDB都是等腰三角形,根据等腰直角三角形的性质得到FH=BH=![]() BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠BOD=2∠BCD,∠A=2∠BCD,
∴∠BOD=∠A,
∵∠AED=∠ABC,
∴∠BOD+∠AED=90°,
∴∠ODE=90°,
即OD⊥DE,
∴DE与⊙O相切;
(2)解:连接BD,过D作DH⊥BF于H,
∵DE与⊙O相切,
∴∠BDE=∠BCD,
∵∠AED=∠ABC,
∴∠AFC=∠DBF,
∵∠AFC=∠DFB,
∴△ACF与△FDB都是等腰三角形,
∴FH=BH=![]() BF=1,则FH=1,由勾股定理可得HD==3,
BF=1,则FH=1,由勾股定理可得HD==3,
在Rt△ODH中,OH2+DH2=OD2,
即(OD﹣1)2+32=OD2,
∴OD=5,
∴⊙O的半径是5.


科目:初中数学 来源: 题型:
【题目】几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=![]() .
.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着电影《流浪地球》的热映,科幻大神刘慈欣的著作受到广大书迷的追捧,《流浪地球》《球状闪电》《三体》《超新星纪元》四部小说在某网上书城热销.已知《流浪地球》的销售单价与《球状闪电》相同,《三体》的销售单价是《超新星纪元》单价的3倍,《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;若自电影上映以来,《流浪地球》与《超新星纪元》的日销售量相同,《球状闪电》的日销售量为《三体》日销售量的3倍,《流浪地球》与《三体》的日销售量和为450本,且《流浪地球》的日销售量不低于《三体》的日销量的![]() 且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
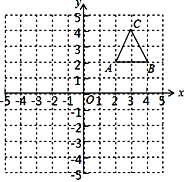
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出A1的坐标;
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并求出点C在旋转过程中经过的路径长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
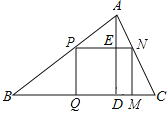
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
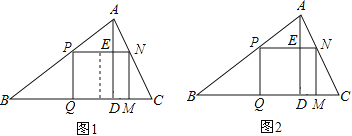
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
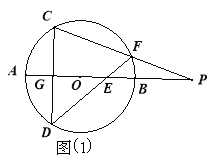
(1)如图1,当点E在直径AB上时,试证明:![]()
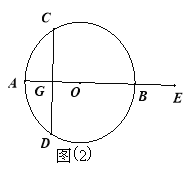
(2)当点E在直径AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com