
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的乘除法和减法可以解答本题;
(3)根据有理数的乘法和加减法可以解答本题;
(4)先把除法转化为乘法,然后按照乘法的分配律即可解答本题.
解答 解:(1)(-1$\frac{3}{4}$)-(+6$\frac{1}{3}$)-2.25+$\frac{10}{3}$
=(-1$\frac{3}{4}$)+(-6$\frac{1}{3}$)+(-2$\frac{1}{4}$)+$\frac{10}{3}$
=-7;
(2)-9×(-11)-3÷(-3)
=99+1
=100;
(3)8×(-$\frac{2}{5}$)-(-4)×(-$\frac{2}{9}$)+(-8)×$\frac{3}{5}$
=$-\frac{16}{5}-\frac{8}{9}-\frac{24}{5}$
=$-8\frac{8}{9}$;
(4 )($\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$)÷(-$\frac{1}{24}$)
=($\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$)×(-24)
=$\frac{1}{2}×(-24)+\frac{5}{6}×(-24)-\frac{7}{12}×(-24)$
=(-12)+(-20)+14
=-18.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6050 | B. | 6049 | C. | 6048 | D. | 6047 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x-2)2+1 | B. | y=3(x+2)2-1 | C. | y=3(x-2)2-1 | D. | y=3(x+2)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm,∠ADB=100°,则∠AEC=100°,AC=12cm.
如图所示,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm,∠ADB=100°,则∠AEC=100°,AC=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
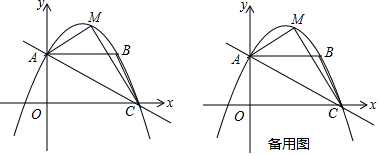
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com