
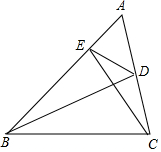
 如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC.
如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC. 科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
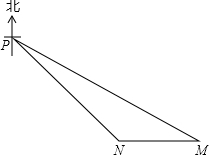 如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.
如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
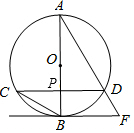 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点P为AB上一个动点,以DP为折线翻折△APD得到△DPE,A的对应点为点E,连接BE,若AB=3,AD=4,当△BEP为直角三角形时,求AP的长.
如图,在矩形ABCD中,点P为AB上一个动点,以DP为折线翻折△APD得到△DPE,A的对应点为点E,连接BE,若AB=3,AD=4,当△BEP为直角三角形时,求AP的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com