
”¾ĢāÄæ”抔ŗģŠĒĘŚĢģ“Ó¼ŅĄļ³ö·¢Ęļ³µČ„¾Ė¾Ė¼Ņ×öæĶ£¬µ±ĖżĘļĮĖŅ»¶ĪĀ·Ź±£¬ĻėĘšŅŖĀņøöĄńĪļĖĶøų±ķµÜ£¬ÓŚŹĒÓÖÕŪ»Ųµ½øÕ¾¹żµÄŅ»¼ŅÉĢµź£¬ĀņŗĆĄńĪļŗóÓÖ¼ĢŠųĘļ³µČ„¾Ė¾Ė¼Ņ£¬ŅŌĻĀŹĒĖż±¾“ĪČ„¾Ė¾Ė¼ŅĖłÓƵď±¼äÓėĀ·³ĢµÄ¹ŲĻµŹ½Ź¾ŅāĶ¼£®øł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
(1)Š”ŗģ¼Ņµ½¾Ė¾Ė¼ŅµÄĀ·³ĢŹĒ______Ć×£¬Š”ŗģŌŚÉĢµźĶ£ĮōĮĖ______·ÖÖÓ£»
(2)ŌŚÕūøöČ„¾Ė¾Ė¼ŅµÄĶ¾ÖŠÄÄøöŹ±¼ä¶ĪŠ”ŗģĘļ³µĖŁ¶Č×īæģ£¬×īæģµÄĖŁ¶ČŹĒ¶ąÉŁĆ×/·Ö
(3)±¾“ĪČ„¾Ė¾Ė¼ŅµÄŠŠ³ĢÖŠ£¬Š”ŗģŅ»¹²ŠŠŹ»ĮĖ¶ąÉŁĆ×£æŅ»¹²ÓĆĮĖ¶ąÉŁ·ÖÖÓ£æ

”¾“š°ø”æ(1)1500£¬4£»(2)Š”ŗģŌŚ12©14·ÖÖÓ×īæģ£¬ĖŁ¶ČĪŖ450Ć×/·Ö£»(3)Š”ŗģ¹²ŠŠŹ»ĮĖ2700Ć×£¬¹²ÓĆĮĖ14·ÖÖÓ£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĶ¼Ļó£¬Ā·³ĢµÄ×ī“óÖµ¼“ĪŖŠ”ŗģ¼Ņµ½¾Ė¾Ė¼ŅµÄĀ·³Ģ£»¶ĮĶ¼£¬¶ŌÓ¦ĢāŅāÕŅµ½ĘäŌŚÉĢµźĶ£ĮōµÄŹ±¼ä¶Ī£¬½ų¶ųæɵĆĘäŌŚŹéµźĶ£ĮōµÄŹ±¼ä£»
£Ø2£©·ÖĪöĶ¼Ļó£¬ÕŅŗÆŹż±ä»Æ×īæģµÄŅ»¶Ī£¬æɵƊ”Ć÷Ęļ³µĖŁ¶Č×īæģµÄŹ±¼ä¶Ī£¬½ų¶ųæɵĆĘäĖŁ¶Č£»
£Ø3£©·ÖæŖŹ¼ŠŠŹ»µÄĀ·³Ģ£¬ÕŪ»ŲÉĢµźŠŠŹ»µÄĀ·³ĢŅŌ¼°“ÓÉĢµźµ½¾Ė¾Ė¼ŅŠŠŹ»µÄĀ·³ĢČż¶ĪĻą¼Ó¼“æÉĒóµĆŠ”ŗģŅ»¹²ŠŠŹ»Ā·³Ģ£»¶ĮĶ¼¼“æÉĒóµĆ±¾“ĪČ„¾Ė¾Ė¼ŅµÄŠŠ³ĢÖŠ£¬Š”ŗģŅ»¹²ÓƵď±¼ä£®
½ā£ŗ(1)øł¾ŻĶ¼Ļó¾Ė¾Ė¼Ņׯ×ų±źĪŖ1500£¬Š”ŗģ¼ŅµÄׯ×ų±źĪŖ0£¬¹ŹŠ”ŗģ¼Ņµ½¾Ė¾Ė¼ŅµÄĀ·³ĢŹĒ1500Ć×£»¾ŻĢāŅā£¬Š”ŗģŌŚÉĢµźĶ£ĮōµÄŹ±¼äĪŖ“Ó8·Öµ½12·Ö£¬¹ŹŠ”ŗģŌŚÉĢµźĶ£ĮōĮĖ4·ÖÖÓ£®
¹Ź“š°øĪŖ£ŗ1500£¬4£»
(2)øł¾ŻĶ¼Ļó£¬12”Üx”Ü14Ź±£¬Ö±Ļß×ī¶ø£¬
¹ŹŠ”ŗģŌŚ12©14·ÖÖÓ×īæģ£¬ĖŁ¶ČĪŖ![]() £½450Ć×/·Ö£®
£½450Ć×/·Ö£®
(3)¶ĮĶ¼æÉµĆ£ŗŠ”ŗģ¹²ŠŠŹ»ĮĖ1200+600+900£½2700Ć×£¬¹²ÓĆĮĖ14·ÖÖÓ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Ó¼×ѧŠ£µ½ŅŅѧŠ£ÓŠA1”¢A2”¢A3ČżĢõĻßĀ·£¬“ÓŅŅѧŠ£µ½±ūѧŠ£ÓŠB1”¢B2¶žĢõĻßĀ·£®
£Ø1£©ĄūÓĆŹ÷דĶ¼»ņĮŠ±ķµÄ·½·Ø±ķŹ¾“Ó¼×ѧŠ£µ½±ūѧŠ£µÄĻßĀ·ÖŠĖłÓŠæÉÄܳöĻֵĽį¹ū£»
£Ø2£©Š”ÕÅČĪŅā×ßĮĖŅ»Ģõ“Ó¼×ѧŠ£µ½±ūѧŠ£µÄĻßĀ·£¬ĒóŠ”ÕÅĒ”ŗĆ¾¹żĮĖB1ĻßĀ·µÄøÅĀŹŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AB”ĪCD£¬”Ļ1=”Ļ2£¬DB=DC£®
£Ø1£©ĒóÖ¤£ŗ”÷ABD”Õ”÷EDC£»
£Ø2£©Čō”ĻA=135”ć£¬”ĻBDC=30”ć£¬Ēó”ĻBCEµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖµćEŗĶµćF·Ö±šŌŚÖ±ĻßABŗĶCDÉĻ£¬ELŗĶFG·Ö±šĘ½·Ö”ĻBEFŗĶ”ĻEFC£¬EL”ĪFG.
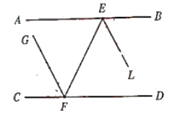
(1)ĒóÖ¤£ŗAB”ĪCD£»
(2)ČēĶ¼£¬µćMĪŖFDÉĻŅ»µć£¬”ĻBEM£¬”ĻEFDµÄ½ĒĘ½·ÖĻßEH£¬FHĻą½»ÓŚµćH£¬Čō”ĻH=”ĻFEM+15”ć£¬ŃÓ³¤HE½»FGÓŚGµć£¬Ēó”ĻGµÄ¶ČŹż£»
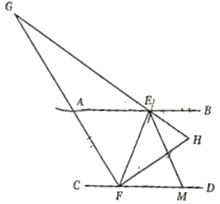
(3)ČēĶ¼£¬µćNŌŚÖ±ĻßABŗĶÖ±ĻßCDÖ®¼ä£¬ĒŅEN”ĶFN£¬µćPĪŖÖ±ĻßABÉĻµÄµć£¬Čō”ĻEPF£¬”ĻPFNµÄ½ĒĘ½·Ö¼¶½»ÓŚµćQ£¬Éč”ĻBEN=¦Į£¬Ö±½ÓŠ“³ö”ĻPQFµÄ“óŠ”ĪŖ(ÓĆŗ¬¦ĮµÄŹ½×Ó±ķŹ¾).
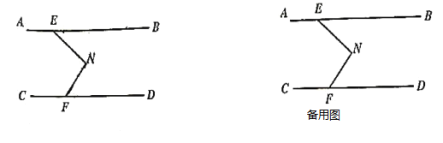
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
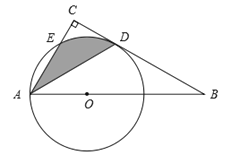
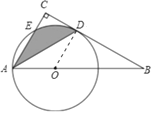
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻBAC=60”ć£¬µćOĪŖRt”÷ABCŠ±±ßABÉĻµÄŅ»µć£¬ŅŌOAĪŖ°ė¾¶µÄ”ŃOÓėBCĒŠÓŚµćD£¬ÓėAC½»ÓŚµćE£¬Į¬½ÓAD.
£Ø1£©Ēó”ĻCADµÄ¶ČŹż£»
£Ø2£©ČōOA = 2£¬ĒóŅõÓ°²æ·ÖµÄĆ껿£Ø½į¹ū±£Įō¦Š£©.
”¾“š°ø”æ£Ø1£©”ĻCADµÄ¶ČŹżĪŖ30”ć£»
£Ø2£©ŅõÓ°²æ·ÖµÄĆ껿ĪŖ![]() .
.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Į¬½ÓOD£®ÓÉĒŠĻߵĊŌÖŹæÉÖŖOD”ĶBC£¬“Ó¶ųæÉÖ¤Ć÷AC”ĪOD£¬ÓÉĘ½ŠŠĻߵĊŌÖŹŗĶµČŃüČż½ĒŠĪµÄŠŌÖŹæÉÖ¤Ć÷”ĻCAD=”ĻOAD£»£Ø2£©Į¬½ÓOE£¬ED”¢OD£®ĻČÖ¤Ć÷ED”ĪAO£¬Č»ŗóŅĄ¾ŻĶ¬µ×µČøßµÄĮ½øöČż½ĒŠĪµÄĆ껿ĻąµČæÉÖŖS”÷AED=S”÷EDO£¬ÓŚŹĒ½«ŅõÓ°²æ·ÖµÄĆ껿æÉ×Ŗ»ÆĪŖÉČŠĪEODµÄĆ껿Ēó½ā¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©Į¬½ÓOD£¬
”ßBCŹĒ”ŃOµÄĒŠĻߣ¬DĪŖĒŠµć£¬
”ąOD”ĶBC.
ÓÖ”ßAC”ĶBC£¬
”ąOD”ĪAC£¬
”ą”ĻADO=”ĻCAD.
ÓÖ”ßOD=OA£¬
”ą”ĻADO=”ĻOAD£¬
”ą”ĻCAD=”ĻOAD=30”ć.
£Ø2£©Į¬½ÓOE£¬ED.

”ß”ĻBAC=60”ć£¬OE=OA£¬
”ą”÷OAEĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻAOE=60”ć£¬
”ą”ĻADE=30”ć.
ÓÖ”ß![]() £¬
£¬
”ą”ĻADE=”ĻOAD£¬
”ąED”ĪAO£¬
”ą![]()
”ąŅõÓ°²æ·ÖµÄĆ껿 = ![]() .
.
”¾ĢāŠĶ”æ½ā“šĢā
”¾½įŹų”æ
6
”¾ĢāÄæ”æČēĶ¼ŹĒÓÉĮ½øö³¤·½Ģå×éŗĻ¶ų³ÉµÄŅ»øöĮ¢ĢåĶ¼ŠĪµÄČżŹÓĶ¼£¬øł¾ŻĶ¼ÖŠĖł±ź³ß“ē£Øµ„Ī»£ŗmm£©£¬ĒóÕāøöĮ¢ĢåĶ¼ŠĪµÄ±ķĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() ÓėxÖį£¬yÖį·Ö±š½»ÓŚA£¬BĮ½µć£¬µć
ÓėxÖį£¬yÖį·Ö±š½»ÓŚA£¬BĮ½µć£¬µć![]() ĪŖÖ±Ļß
ĪŖÖ±Ļß![]() ÉĻŅ»µć£¬Ö±Ļß
ÉĻŅ»µć£¬Ö±Ļß![]() ¹żµćC£®
¹żµćC£®

![]() ĒómŗĶbµÄÖµ£»
ĒómŗĶbµÄÖµ£»
![]() Ö±Ļß
Ö±Ļß![]() ÓėxÖį½»ÓŚµćD£¬¶ÆµćP“ÓµćDæŖŹ¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņxÖįøŗ·½ĻņŌĖ¶Æ
ÓėxÖį½»ÓŚµćD£¬¶ÆµćP“ÓµćDæŖŹ¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņxÖįøŗ·½ĻņŌĖ¶Æ![]() ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
¢ŁČōµćPŌŚĻ߶ĪDAÉĻ£¬ĒŅ![]() µÄĆ껿ĪŖ10£¬ĒótµÄÖµ£»
µÄĆ껿ĪŖ10£¬ĒótµÄÖµ£»
¢ŚŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹![]() ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Ö±½ÓŠ“³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Ö±½ÓŠ“³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬DŹĒBCµÄÖŠµć£¬¹żDµćµÄÖ±ĻßGF½»ACÓŚF£¬½»ACµÄĘ½ŠŠĻßBGÓŚGµć£¬DE”ĶDF£¬½»ABÓŚµćE£¬Į¬½įEG”¢EF£®

£Ø1£©ĒóÖ¤£ŗBG£½CF£®
£Ø2£©ĒėÄćÅŠ¶ĻBE+CFÓėEFµÄ“󊔹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
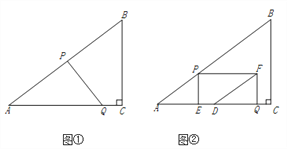
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬AB=10£¬BC=6£®µćP“ÓµćA³ö·¢£¬ŃŲÕŪĻÖAB”ŖBCĻņÖÕµćCŌĖ¶Æ£¬ŌŚABÉĻŅŌĆæĆė5øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬ŌŚBCÉĻŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£®µćQ“ÓµćC³ö·¢£¬ŃŲCA·½ĻņŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£®µćP”¢QĮ½µćĶ¬Ź±³ö·¢£¬µ±µćPĶ£Ö¹Ź±£¬µćQŅ²ĖęÖ®Ķ£Ö¹£®ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖtĆė£®
øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£®µćP”¢QĮ½µćĶ¬Ź±³ö·¢£¬µ±µćPĶ£Ö¹Ź±£¬µćQŅ²ĖęÖ®Ķ£Ö¹£®ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖtĆė£®
£Ø1£©ĒóĻ߶ĪAQµÄ³¤£®£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©
£Ø2£©µ±PQÓė”÷ABCµÄŅ»±ßĘ½ŠŠŹ±£¬ĒótµÄÖµ
£Ø3£©ČēĶ¼¢Ś£¬¹żµćP×÷PE”ĶACÓŚµćE£¬ŅŌPE”¢QEĪŖĮŚ±ß×÷¾ŲŠĪPEQF£¬µćDĪŖACµÄÖŠµć£¬Į¬½įDF£®Ö±½ÓŠ“³öDF½«¾ŲŠĪPEQF·Ö³ÉĮ½²æ·ÖµÄĆ껿±ČĪŖ1:2Ź±tµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬ŅŌµćAĪŖŌ²ŠÄ£¬AB³¤ĪŖ°ė¾¶»»”½»ADÓŚµćF£¬ŌŁ·Ö±šŅŌµćB”¢FĪŖŌ²ŠÄ£¬“óÓŚ![]() ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚŅ»µćP£¬Į¬½ÓAP²¢ŃÓ³¤½»BCÓŚµćE£¬Į¬½ÓEF£®
³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚŅ»µćP£¬Į¬½ÓAP²¢ŃÓ³¤½»BCÓŚµćE£¬Į¬½ÓEF£®

£Ø1£©ĖıߊĪABEFŹĒ_______£»£ØŃ”Ģī¾ŲŠĪ”¢ĮāŠĪ”¢Õż·½ŠĪ”¢ĪŽ·ØČ·¶Ø£©£ØÖ±½ÓĢīŠ“½į¹ū£©
£Ø2£©AE£¬BFĻą½»ÓŚµćO£¬ČōĖıߊĪABEFµÄÖܳ¤ĪŖ40£¬BF=10£¬ŌņAEµÄ³¤ĪŖ________£¬”ĻABC=________”ć£®£ØÖ±½ÓĢīŠ“½į¹ū£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com