练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：（）﹣2+（π﹣2014）0+sin60°+|﹣2|．


    原式=9+1++2﹣

    =12﹣；


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    2013年我国GDP总值为56.9万亿元，增速达7.7%，将56.9万亿元用科学记数法表示为（　　）

    　

    A．

    56.9×1012元

    B．

    5.69×1013元

    C．

    5.69×1012元

    D．

    0.569×1013元

    查看答案和解析>>

    科目：初中数学 来源： 题型：


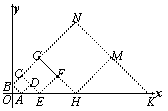
    如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=OB=a，以线段AB为边在第一象限作正方形ABCD，CD的延长线交x轴于点E，再以CE为边作第二个正方形ECGF，…，依此方法作下去，则第n个正方形的边长是         .

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知如图，一次函数y=ax+b和反比例函数y=的图象相交于A、B两点，不等式ax+b＞的解集为（　　）

    　 

    A． x＜﹣3          B． ﹣3＜x＜0或x＞1 C． x＜﹣3或x＞1    D． ﹣3＜x＜1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    四边形的内角和为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点P（x0，y0）和直线y=kx+b，则点P到直线y=kx+b的距离d可用公式d=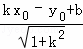计算．

    例如：求点P（﹣2，1）到直线y=x+1的距离．

    解：因为直线y=x+1可变形为x﹣y+1=0，其中k=1，b=1．

    所以点P（﹣2，1）到直线y=x+1的距离为d====．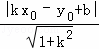

    根据以上材料，求：

    （1）点P（1，1）到直线y=3x﹣2的距离，并说明点P与直线的位置关系；

    （2）点P（2，﹣1）到直线y=2x﹣1的距离；

    （3）已知直线y=﹣x+1与y=﹣x+3平行，求这两条直线的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    不等式3x+2＞﹣1的解集是（　　）

    　  A．             x＞﹣             B． x＜﹣          C． x＞﹣1   D． x＜﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．

    （1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．

    （2）探究下列问题：

    ①若一个函数的特征数为[4，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．

    ②若一个函数的特征数为[2，3]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[3，4]？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（　　）

    　

    A．

    （6+6）米

    B．

    （6+3）米

    C．

    （6+2）米

    D．

    12米

    查看答案和解析>>

    同步练习册答案