
 已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).
已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).分析 (1)将A、B、C三点坐标代入y=ax2+bx+c,可得抛物线解析式,继而可得顶点M的坐标;
(2)过点M作MD⊥x轴于点D,则S四边形ABMC=S△AOC+S梯形OCMD+S△MBD,分别计算即可.
(3)根据函数的图象及A、C的位置,可明显的看出∠APC不可能是直角,因此此题要分两种情况讨论:
①∠PAC=90°,设出点P的坐标,然后表示出AC2、PA2、PC2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标.
解答 解:(1)将A(-1,0)、B(2,0)、C(0,-2)代入抛物线解析式,
得:$\left\{\begin{array}{l}{a-b+c=0}\\{4a+2b+c=0}\\{c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-1}\\{c=-2}\end{array}\right.$,
故抛物线解析式为y=x2-x-2,
∵y=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$
∴顶点坐标为($\frac{1}{2}$,-$\frac{9}{4}$).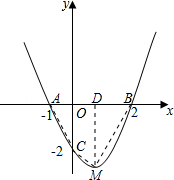 (2)连接AC、CM、BM,过点M作MD⊥x轴于点D,
(2)连接AC、CM、BM,过点M作MD⊥x轴于点D,
则S四边形ABMC=S△AOC+S梯形OCMD+S△MBD
=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2+$\frac{9}{4}$)×$\frac{1}{2}$+$\frac{1}{2}$×$\frac{3}{2}$×$\frac{9}{4}$
=1+$\frac{17}{16}$+$\frac{27}{16}$
=$\frac{15}{4}$.
(3)假设存在符合条件的点P,设点P的坐标为P(m,n),则m>$\frac{1}{2}$且n=m2-m-2;
PA2=(m+1)2+n2,PC2=m2+(n+2)2,AC2=5,
分以下几种情况讨论:
①若∠PAC=90°,则PC2=PA2+AC2.
∴$\left\{\begin{array}{l}{n={m}^{2}-m-2}\\{{m}^{2}+(n+2)^{2}=(m+1)^{2}+{n}^{2}+5}\end{array}\right.$,
解得m1=$\frac{5}{2}$,m2=-1;
∵m>$\frac{1}{2}$,
∴m=$\frac{5}{2}$,
∴P1($\frac{5}{2}$,$\frac{7}{4}$);
②若∠PCA=90°,则PA2=PC2+AC2
∴$\left\{\begin{array}{l}{n={m}^{2}-m-2}\\{(m+1)^{2}+{n}^{2}={m}^{2}+(n+2)^{2}+5}\end{array}\right.$,
解得m3=$\frac{3}{2}$,m4=0,
∵m>$\frac{1}{2}$,
∴m=$\frac{3}{2}$,
∴P2($\frac{3}{2}$,-$\frac{5}{4}$);
当点P在对称轴右侧时,PA>AC,
所以边AC的对角∠APC不可能是直角,
故存在符合条件的点P,且坐标为P1($\frac{5}{2}$,$\frac{7}{4}$),P2($\frac{3}{2}$,-$\frac{5}{4}$).
点评 此题是二次函数的综合题,考查了二次函数顶点坐标及函数图象与坐标轴交点坐标的求法、图形面积的求法、直角三角形的判定、勾股定理等知识,要注意的是(3)题一定要根据不同的直角顶点分类讨论,以免漏解.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=60°,AD,BE分别平分∠CAB,∠CBA、AD、BE交于点P.求证:
如图,△ABC中,∠C=60°,AD,BE分别平分∠CAB,∠CBA、AD、BE交于点P.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
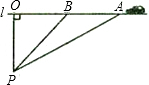 据交管部门统计,超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,双龙大道某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由江宁东山向禄口机场匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
据交管部门统计,超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,双龙大道某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由江宁东山向禄口机场匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com