
 如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.
如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.分析 (1)依题意补全图形;
(2)由平行得内错角相等,再根据同角的余角相等得结论;
(3)作辅助线,构建全等三角形,证明△ABG≌△ADH,得AG=AH,且得△AGH是等腰直角三角形,得
GH=$\sqrt{2}$AG,则DG=DH+GH=$\sqrt{2}$AG+BG.
解答 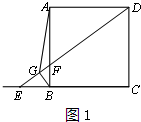 解:(1)补全图形,如图1;
解:(1)补全图形,如图1;
(2)证明∵正方形ABCD,
∴AD∥BC,
∴∠DEC=∠ADE,
∵∠ABC=90°,
∴∠FBE=90°,
∴∠ABG+∠EBG=90°,
∵BG⊥DE于点G,
∴∠DEC+∠EBG=90°,
∴∠ABG=∠DEC,
∴∠ABG=∠ADE;
(3)DG=$\sqrt{2}$AG+BG,理由是:
如图2,在DE上截取DH=BG,连接AH,
∵四边形ABCD是正方形,
∴∠DAB=90°,AB=AD,
∵∠ABG=∠ADH(已证),
∴△ABG≌△ADH(SAS),
∴AG=AH,∠GAB=∠HAD,
∴∠GAH=90°,
∴AG2+AH2=GH2,
∴GH=$\sqrt{2}$AG,
∴DG=DH+GH=$\sqrt{2}$AG+BG.
点评 本题考查了正方形、全等三角形的性质和判定,运用了勾股定理证明线段之间的关系;在几何证明中常常会添加辅助线,本题是截取线段相等,构建了两个三角形全等,把三条线段的位置转化到同一条线段上,使问题得以解决.


科目:初中数学 来源: 题型:填空题
 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.
如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
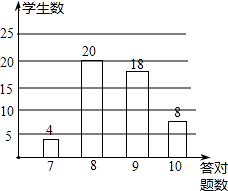 数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )
数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )| A. | 0.38 | B. | 0.4 | C. | 0.16 | D. | 0.08 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com