
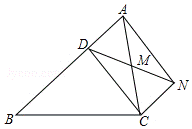
 已知:如图,D是△ABC的边上一点,M是AC的中点,CN∥AB交DM的延长线于N,且AB=10,BC=8,AC=7.
已知:如图,D是△ABC的边上一点,M是AC的中点,CN∥AB交DM的延长线于N,且AB=10,BC=8,AC=7.分析 (1)根据两直线平行,内错角相等可得∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)根据矩形的四个角都是直角可得CD⊥AB,设AD=x,然后在两个直角三角形中利用勾股定理表示出CD2并得到方程求解即可.
解答 (1)证明:∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,$\left\{\begin{array}{l}∠DAC=∠NCA\\ MA=MC\\∠AMD=∠CMN\end{array}\right.$,
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形;
(2)解:若四边形ADCN是矩形,则CD⊥AB,
设AD=x,则CD2=49-x2=64-(10-x)2,
100-20x=15,
解得x=$\frac{17}{4}$,
所以,AD=$\frac{17}{4}$.
点评 本题考查了矩形的判定,平行四边形的判定与性质,平行线的性质以及全等三角形的判定与性质,熟练掌握矩形以及平行四边形的判定方法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
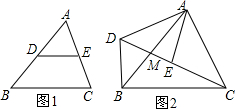 如图1,在△ABC中,D点在边AB上,E点在边AC上,DE∥BC将△ADE绕A点沿顺时针方向旋转30°,使得D、E、C三点在一条直线上,AB与CD交于M点,连接BD,如图2.
如图1,在△ABC中,D点在边AB上,E点在边AC上,DE∥BC将△ADE绕A点沿顺时针方向旋转30°,使得D、E、C三点在一条直线上,AB与CD交于M点,连接BD,如图2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
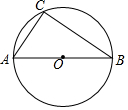 已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B﹦90°,AB﹦8cm,AD﹦24cm,BC﹦26cm,点p从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t s.
如图,在四边形ABCD中,AD∥BC,∠B﹦90°,AB﹦8cm,AD﹦24cm,BC﹦26cm,点p从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
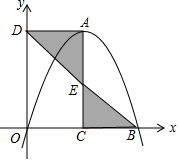 如图,在平面直角坐标系中,抛物线y=-x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为4.
如图,在平面直角坐标系中,抛物线y=-x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com