
 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余分析 (1)①若m=60,m°+n°=90°,n=30,则射线OC的方向是北偏东30°;
②根据和为90°的两个角互余,可得答案,根据两个角的和为180°,这两个角互补,可得答案;
(2)根据OA是∠BON的角平线,可得∠NOA与∠NOB的关系,根据两角互补,可得∠BON与∠SOB的关系,再根据角平分线,可得∠NOA与∠NOB的关系,根据两角互余,可得∠NOC与∠SOB的关系,根据角的和差,可得答案.
解答 解:(1)①若m=60,m°+n°=90°,n=30,
则射线OC的方向是北偏东30°;
故答案为:北偏东30°.
②∵∠BOS+∠BOE=90°,∴图中与∠BOE互余的角有∠BOS,
∵由m°的角与n°的角互余,∠BOE+COE=90°,
∴得图中与∠BOE互余的角有∠COE,
∴与∠BOE互余的角有∠COE、∠BOS,
∵∠BOE+BOW=180°,∠BOE+∠SOC=180°
∴∠BOE互补的角有∠BOW、∠SOC
(2)∠AOC=$\frac{1}{2}{m}^{°}$.
∵射线OA是∠BON的角平分线,
∴∠NOA=$\frac{1}{2}$∠NOB,
∵∠SOB+∠BON=180°,
∠BON=180°-∠SOB,
∠NOA=$\frac{1}{2}$∠BON=90°-$\frac{1}{2}$∠SOB,
∵∠NOC+∠SOB=90°,∠NOC=90°-∠SOB,
∠AOC=N0A-∠NOC=90°-$\frac{1}{2}$∠SOB-(90°-∠SOB)
∠AOC=$\frac{1}{2}$∠SOB=$\frac{1}{2}{m}^{°}$.
点评 本题考查了方向角,余角、补角是解(1)题的关键,(2)先求∠NOA与∠NOB的关系,根据两角互补,可得∠BON与∠SOB的关系,再根据角平分线,可得∠NOA与∠NOB的关系,根据两角互余,可得∠NOC与∠SOB的关系,根据角的和差,可得答案.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
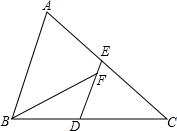 如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )
如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )| A. | 2 | B. | 3 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,BD平分∠ABC,DE平分∠ADB,且DE∥BC.
如图,在△ABC中,BD平分∠ABC,DE平分∠ADB,且DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
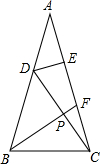 如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )
如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )| A. | 36° | B. | 54° | C. | 72° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com