
【题目】如图,在数轴上点A,点B,点C表示的数分别为﹣2,1,6.
![]()
(1)线段AB的长度为 个单位长度,线段AC的长度为 个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为 个单位长度,点P在数轴上表示的数为 ;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
【答案】(1)3;8;(2)(3﹣t)或(t﹣3);﹣2+t;(3)x=3;M在数轴上表示的数是10.
【解析】
(1)根据两点间的距离公式可求线段AB的长度,线段AC的长度;
(2)先根据路程=速度×时间求出点P运动的路程,再分点P在点B的左边和右边两种情况求解;
(3)根据等量关系点M、N两点间的距离为13个单位长度列出方程求解即可.
(1)线段AB的长度为1﹣(﹣2)=3个单位长度,线段AC的长度为6﹣(﹣2)=8个单位长度;
(2)线段BP的长为:当t≤3时,BP=3﹣t;当t>3时,BP=t﹣3,点P在数轴上表示的数为﹣2+t;
(3)∵AC=8<13,∴M、N相遇后再走13个单位长度,依题意有:
4x+3x﹣8=13
解得:x=3.
此时点M在数轴上表示的数是﹣2+4×3=10.
故答案为:(1)3;8;(2)(3﹣t)或(t﹣3);﹣2+t.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,无论k取何实数,直线y=(k-1)x+4-5k总经过定点P,则点P与动点Q(5m-1,5m+1)的距离的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= ![]() 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.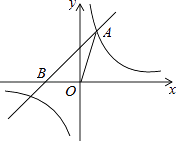
(1)求k和b的值;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
A.ac>0
B.b+2a<0
C.b2﹣4ac>0
D.a﹣b+c<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(![]() ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com