
【题目】已知y=|y1|+y2﹣1,其中y1=x﹣3,y2与x成反比例关系,且当x=2时,y2=3.
(1)根据给定的条件写出y与x的函数表达式及自变量x的取值范围: .
(2)当x>0时,根据y与x的函数表达式,选取适当的自变量x的值,完成下表,并根据表中数据,在平面直角坐标系xOy中描点,画出该函数x>0时的图象.
x | …… | …… | |||||||
y | …… | …… |
(3)当x>0时,结合函数图象,解决相关问题:估计y=﹣![]() x+5时,x的值约为 .(保留一位小数)
x+5时,x的值约为 .(保留一位小数)
【答案】(1)y=|x﹣3|+![]() ﹣1,(x≠0);(2)见解析;(3)1.6或5.5.
﹣1,(x≠0);(2)见解析;(3)1.6或5.5.
【解析】
(1)设y2=![]() ,则y=|y1|+y2﹣1=|x﹣3|+
,则y=|y1|+y2﹣1=|x﹣3|+![]() ﹣1,代入x=2时,y2=3,即可求出k,即可得出y与x的函数表达式及自变量x的取值范围;
﹣1,代入x=2时,y2=3,即可求出k,即可得出y与x的函数表达式及自变量x的取值范围;
(2)列表,描点画图;
(3)估计y=﹣![]() x+5时,结合函数图象即可求得x的值.
x+5时,结合函数图象即可求得x的值.
(1)y2与x成反比例,
设y2=![]() ,
,
∴y=|y1|+y2﹣1=|x﹣3|+![]() ﹣1,
﹣1,
∵当x=2时,y2=3,
∴3=|2﹣3|+![]() ﹣1,
﹣1,
∴k=6,
∴y=|x﹣3|+![]() ﹣1,(x≠0),
﹣1,(x≠0),
故答案为y=|x﹣3|+![]() ﹣1,(x≠0);
﹣1,(x≠0);
(2)当x>0时,完成下表:
x | …… | 1 | 2 | 3 | 4 | 5 | 6 | 7 | …… |
y | …… | 7 | 3 | 1 |
|
| 3 |
| …… |
画出图象如图:
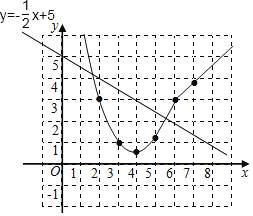
(3)结合函数图象可知,估计y=﹣![]() x+5时,x的值约为1.6或5.5,
x+5时,x的值约为1.6或5.5,
故答案为1.6或5.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
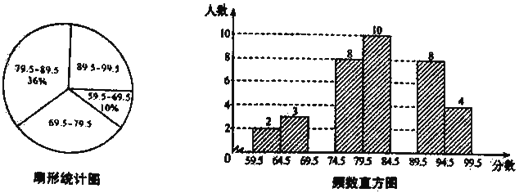
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a使关于x的分式方程![]() 的解为整数,且使关于y的不等式组
的解为整数,且使关于y的不等式组![]() 有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
A.﹣3B.﹣8C.﹣13D.﹣17
查看答案和解析>>
科目:初中数学 来源: 题型:
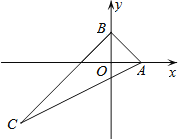
【题目】如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=![]() x﹣
x﹣![]() ,若△ABC的内心在y轴上,则tan∠ACB的值为( )
,若△ABC的内心在y轴上,则tan∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
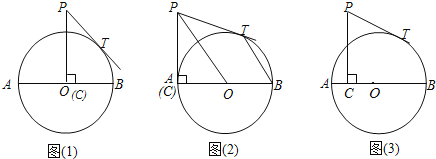
(1)如图1,当C点运动到O点时,求PT的长;
(2)如图2,当C点运动到A点时,连接PO、BT,求证:PO∥BT;
(3)如图3,设PT=y,AC=x,求y与x的解析式并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
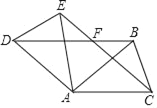
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=![]() ,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com