
����Ŀ��Ϊ�ˡ������������У�������������������ij������Ͻ���ڵ�һ�����Ϊ![]() �Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ
�Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ![]() ���ֲ��������
���ֲ��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ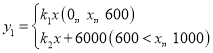 �������ͼ����ͼ��ʾ.�Ի��������
�������ͼ����ͼ��ʾ.�Ի��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() .
.
��1�����![]() ��
��![]() ��ֵ��
��ֵ��
��2�����ֻ������С��![]() ʱ���̻��ܷ���Ϊ
ʱ���̻��ܷ���Ϊ![]() ��Ԫ����д��
��Ԫ����д��![]() ��
��![]() �ĺ�����ϵʽ��������̻��ܷ���
�ĺ�����ϵʽ��������̻��ܷ���![]() �����ֵ.
�����ֵ.
���𰸡���1��![]() ��
��![]() ����2��
����2��![]()
![]() ���̻��ܷ���
���̻��ܷ���![]() �����ֵΪ32500Ԫ.
�����ֵΪ32500Ԫ.
��������
��1����x=600��y=18000����y1=k1x�ɵ�k1����x=1000��y=26000����y1=k2x+6000�ɵ�k2��
��2�������ֻ������С��![]() �����ֲ����С�ڵ���
�����ֲ����С�ڵ���![]() �������ܷ���=�ֲݵķ���+�ֻ��ķ����г����κ�������ʽ��Ȼ�����ݶ��κ��������ʿɵã�
�������ܷ���=�ֲݵķ���+�ֻ��ķ����г����κ�������ʽ��Ȼ�����ݶ��κ��������ʿɵã�
�⣺��1����ͼ���֪����![]() ��
��![]() �ϣ�����ã�
�ϣ�����ã�![]() ��
��
���![]() ��
��
��ͼ���֪����![]() ��
��![]() �ϣ�
�ϣ�
���![]() ��
��
��2�����ֻ������С��![]() ��
��
���ֲ����С�ڵ���![]() ��
��
������ɵã�
![]()
![]()
![]() ��
��
����![]() ʱ��
ʱ��![]() �����ֵΪ32500Ԫ.
�����ֵΪ32500Ԫ.
���̻��ܷ���![]() �����ֵΪ32500Ԫ..
�����ֵΪ32500Ԫ..



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
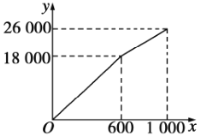
����Ŀ��ͼ����һö�ʵؾ��ȵ�����������״�����ӣ�ÿ�����Ϸֱ��������2��3��4��5��ͼ����һ�������������̣���ͨ�������ӵķ�ʽ��������Ϸ�������ǣ�����ö�����������������������������ϣ������棩�������Ǽ����ʹ�ͼ�е�A�㿪ʼ����˳ʱ�뷽�����������������㣬�ڶ��δӵ�һ�ε��յ㴦��ʼ������һ�εķ�����������
��1�������һ�����ӣ���������������C���ĸ������� ����
��2��������������ӣ��û���״ͼ���б��ķ�����������������������C���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y=ax+b��y=ax2��bx��ͼ������ǣ� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������깺���֧����ʽ�������࣬ij��ѧ��ȤС��ʹ˽����˳������飮��������ʾ��֧����ʽ�У�A�š�B֧������C�ֽ�D��������С���ij����һ���ڹ����ߵ�֧����ʽ���е���ͳ�ƣ��õ�����������������ͳ��ͼ��

�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1������һ�������˶����������ߣ�
��2���벹ȫ����ͳ��ͼ��������ͳ��ͼ��A��֧����ʽ����Ӧ��Բ�Ľ�Ϊ�� ���ȣ�
��3�����ó�����һ������1600�������ߣ��������ʹ��A��B����֧����ʽ�Ĺ����߹��ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬��O��D�ֱ�ΪAB��BC���е㣬����O��AC�����ڵ�E����AC����ȡһ��F��ʹDF��DO.
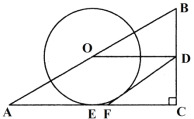
����֤��DF�ǡ�O���ߣ�����sinB��![]() ��CF��2�����O�İ뾶.
��CF��2�����O�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������ϵ�У�����![]() �ı�
�ı�![]() ��
��![]() ���ϣ���
���ϣ���![]() ��ԭ�㣬
��ԭ�㣬![]() .��������ÿ��2����λ������
.��������ÿ��2����λ������![]() ���������������˶�.ͬʱ��
���������������˶�.ͬʱ��![]() �ӵ�
�ӵ�![]() ������ÿ��1����λ������
������ÿ��1����λ������![]() ��·���������˶�����
��·���������˶�����![]() ���˶���
���˶���![]() ��ʱֹͣ�˶�������
��ʱֹͣ�˶�������![]() Ҳ��ֹ֮ͣ�˶�.��
Ҳ��ֹ֮ͣ�˶�.��![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ���룩.
���룩.
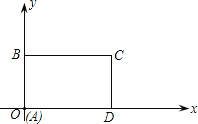
��1����![]() ʱ�������
ʱ�������![]() �����ꣻ
�����ꣻ
��2����![]() �����Ϊ
�����Ϊ![]() �������
�������![]() ��
��![]() ֮��ĺ�����ϵʽ����д����Ӧ���Ա���
֮��ĺ�����ϵʽ����д����Ӧ���Ա���![]() ��ȡֵ��Χ��.
��ȡֵ��Χ��.
��3�������⣨2�����еĺ����Ĵ���ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C��90����AC��4cm��BC��3cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶�һ�ܣ����ٶ�Ϊÿ��2cm�����˶�ʱ��Ϊt�룬��t��_____ʱ����P���ABC��ij�������㹹�ɵ��������Σ�
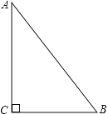
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CA��CB����C��90�㣬��D��BC���е㣬����ABC����ֱ��EF�۵���ʹ��A���D�غϣ��ۺ۽�AB�ڵ�E����AC�ڵ�F����ôsin��BED��ֵΪ��������
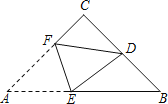
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У�E��AD���е㣬�Ե�Eֱ�Ƕ����ֱ��������EFG������EF��EG�ֱ����B��C����F��30��.
��1����֤��BE��CE
��2������EFG�Ƶ�E��˳ʱ�뷽����ת������ת��EF��AD�غ�ʱֹͣת��.��EF��EG�ֱ���AB��BC�ཻ�ڵ�M��N.����ͼ2��
����֤����BEM�ա�CEN��
����AB��2�����BMN��������ֵ��
�۵���תֹͣʱ����Bǡ����FG�ϣ���ͼ3������sin��EBG��ֵ.
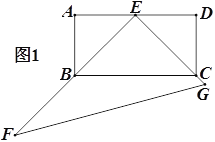
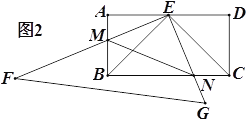
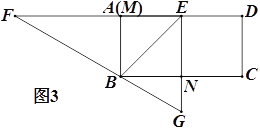
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com