
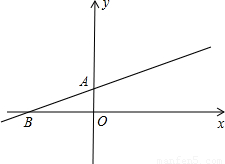
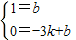 ,
, ,b=1,
,b=1, x+1;
x+1; t+1),
t+1), t+1或-t=
t+1或-t= t+1,
t+1, 或t=-
或t=- ;
;
 t+1),
t+1), t+1,PM=t,根据已知CD=2,则CM=1,
t+1,PM=t,根据已知CD=2,则CM=1,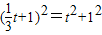 ,
, ,
, ,
, ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.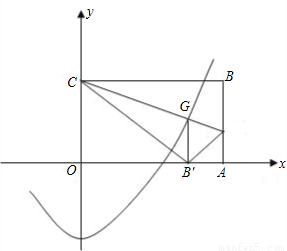
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
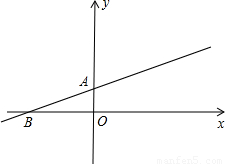
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(01)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2005年广西南宁市中考数学试卷(课标卷)(解析版) 题型:解答题
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com