

分析 ①连接EH,根据折叠得出AB⊥OH,根据切线定理得出HO⊥CD,根据平行线的判定推出即可;
②当点E与点A重合时,即点C与点A重合,求出AD长,即可得出答案.
解答 解:
①当点E与点O重合时,CD∥AB,
理由是:如图1,连接HE,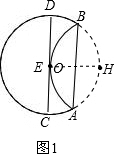
∵OH是半径,CD切⊙H于E,
∴OH⊥CD,
∵OH⊥AB,
∴CD∥AB;
②如图2,当点E与点A重合时,CD=AB=6$\sqrt{3}$,
理由是:连接HD,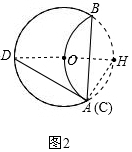
当点E与点A重合时,即点C与点A重合,
∵CD切⊙H于A,
∴HA⊥CD,
∴∠HAD=90°,
∴HD为直径,
即HD=2×6=12,
∵AH=6,
∴在Rt△DAH中,AD=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
即CD=AB=6$\sqrt{3}$.
点评 本题主要考查切线的性质及翻折的性质,画出正确的图形,确定出CD的位置是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
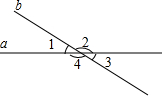 如图,已知直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数
如图,已知直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正三棱柱的面EFDC平行于投影面P,且AE=EF=AF=2,AB=6.
如图,正三棱柱的面EFDC平行于投影面P,且AE=EF=AF=2,AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知每个小方格的边长为1,A、B、C三点都在小方格的顶点上,则点C到AB所在直线的距离等于( )
如图,已知每个小方格的边长为1,A、B、C三点都在小方格的顶点上,则点C到AB所在直线的距离等于( )| A. | $\frac{{\sqrt{10}}}{8}$ | B. | $\frac{8}{{\sqrt{10}}}$ | C. | $\frac{4}{{\sqrt{10}}}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com