【题目】已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线
x 0经过D点，交AB于E点，且OBAC=160，则点E的坐标为（ ）．
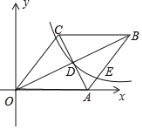
A.（3，8）B.（12，
）C.（4，8）D.（12，4）
期末金牌卷系列答案
轻松课堂标准练系列答案科目：初中数学 来源： 题型：
【题目】如图①，四边形
和四边形
都是正方形，且
，
，正方形固定，将正方形绕点
顺时针旋转
角(
)．
（1）如图②，连接
、
，相交于点
，请判断和是否相等？并说明理由；
（2）如图②，连接
，在旋转过程中，当
为直角三角形时，请直接写出旋转角的度数；
（3）如图③，点
为边
的中点，连接
、
、
，在正方形的旋转过程中，
的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】盒子中有4个球，每个球上写有1～4中的一个数字，不同的球上数字不同．
（1）若从盒中取三个球，以球上所标数字为线段的长，则能构成三角形的概率是多少？
（2）若小明从盒中取出一个球，放回后再取出一个球，然后让小华猜两球上的数字之和，你认为小华猜和为多少时，猜中的可能性大．请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
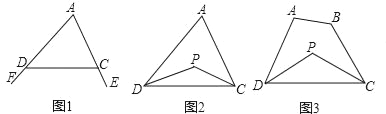
【题目】探究与发现：
探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？
已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．
探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．
探究三：若将△ADC改为任意四边形ABCD呢？
已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
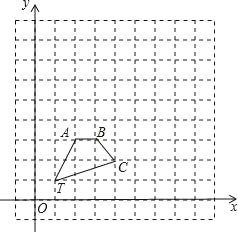
【题目】如图，在正方形网格中，四边形TABC的顶点坐标分别为T（1，1），A（2，3），B（3，3），C（4，2）．
(1)以点T（1，1）为位似中心，在位似中心的同侧将四边形TABC放大为原来的2倍，放大后点A，B，C的对应点分别为A′，B′，C′画出四边形TA′B′C′；
(2)写出点A′，B′，C′的坐标：
A′ ，B′ ，C′ ；
(3)在(1)中，若D（a，b）为线段AC上任一点，则变化后点D的对应点D′的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，∠BAC＝90°，分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE，过点 D 做 FC 的延长线的垂线，垂足为点 H．
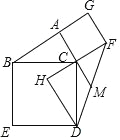
(1)求证：△ABC≌△HDC；
(2)连接 FD，交 AC 的延长线于点 M，若 AG＝
，tan∠ABC＝ 
，求△FCM 的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题中，（1）数轴上的所有点都表示有理数；（2）无理数可以用数轴上的点表示；（3）实数与数轴上的点一一对应；（4）无限小数是无理数；（5）带根号的数都是无理数；（6）数轴上的点不是表示有理数，就是表示无理数；错误命题的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
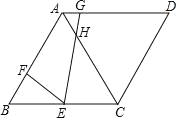
【题目】如图，在菱形ABCD中，∠B＝60°，BC＝6，E为BC中点，F是AB上一点，G为AD上一点，且BF＝2，∠FEG＝60°，EG交AC于点H，下列结论：①△BEF∽△CHE；②AG＝1；③EH＝
；④S△BEF＝3S△AGH；正确的是______．（填序号即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C
处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最
短距离为 ▲ cm．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
