
分析 ①先计算算术平方根、去绝对值符号,再计算加减即可得;
②根据平方根和算术平方根的定义得出x、y、z的值,再代入计算即可得;
③两边都除以3后根据平方根的定义得出x+1的值,继而可得答案;
④根据坐标轴上的点坐标特征,分横坐标与纵坐标为零两种情况讨论求解;
⑤将方程组整理成一般式后,利用加减消元法求解可得.
解答 解:①原式=$\frac{1}{4}$-$\frac{5}{2}$+π-$\sqrt{3}$+$\sqrt{3}$=π-$\frac{9}{4}$;
②由题意得x=5、y=4,z=±3,
当z=3时,2x+y-5z=10+4-15=-1;
当z=-3时,2x+y-5z=10+4+15=29;
③∵3(x+1)2=48,
∴(x+1)2=16,
则x+1=4或x+1=-4,
解得:x=3或x=-5;
④∵点P(m+3,m+1)在坐标轴上,
∴m+3=0或m+1=0,
∴m=-3或m=-1,
∴点P(0,-5)或(-1,0).
⑤整理,得:$\left\{\begin{array}{l}{x-3y=-2}&{①}\\{5x-3y=20}&{②}\end{array}\right.$,
②-①,得:4x=22,
解得:x=$\frac{11}{2}$,
将x=$\frac{11}{2}$代入①,得:$\frac{11}{2}$-3y=-2,
解得:y=$\frac{5}{2}$,
∴方程组的解为$\left\{\begin{array}{l}{x=\frac{11}{2}}\\{y=\frac{5}{2}}\end{array}\right.$.
点评 本题主要考查实数的混合运算、解一元二次方程、二元一次方程组的能力,熟练掌握平方根、算术平方根的定义,绝对值的性质及坐标轴上点的坐标符号特点等知识点是解题的关键.


科目:初中数学 来源: 题型:解答题
| 参加年级 | A组学生 | 其它组学生 | 总数 |
| 参加人数 | x | 65-x | 65 |
| 每人搬椅子 | 6 | 8 | -- |
| 共搬椅子 | 6x | 8(65-x) | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
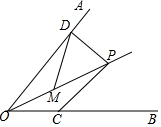 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
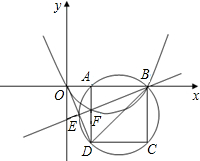 如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.
如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com