
分析 (1)根据根据“派生函数”的定义即可解决问题.
(2)①如图1中,设AB=AC=m,BC=n,由题意△ABC的派生函数为y=mx2-nx+m,只要证明△<0即可.
②如图2中,作AH⊥BC于H.设AB=AC=m,BC=n,n<m.由题意△ABC的派生函数为y=nx2-mx+m,由△ABC的派生函数与x轴有公共点,可得△≥0,推出m2-4mn≥0,推出m≥4n,于cosC=$\frac{HC}{AC}$=$\frac{\frac{1}{2}n}{m}$=$\frac{n}{2m}$,当m=4n时,cosC=$\frac{1}{8}$,由此可得0<cosC≤$\frac{1}{8}$.
③如图3中,首先求出A、B、C坐标,分两种情形确定a的范围即可.
解答 (1)解:根据“派生函数”的定义可知,三角形的边长为3,4,5,
这个三角形的派生函数为y=3x2-5x+4.
故答案为y=3x2-5x+4.
(2)①证明:如图1中,设AB=AC=m,BC=n,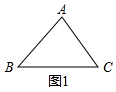
∵∠A=60°,
∴m=m<n,2m>n,
∴△ABC的派生函数为y=mx2-nx+m,
∵△=n2-4m2=(n+2m)(n-2m),
∵n+2m>0,n-2m<0,
∴△<0,
∴△ABC的派生函数与x轴没有公共点.
②解:如图2中,作AH⊥BC于H.设AB=AC=m,BC=n,n<m.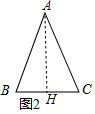
∴△ABC的派生函数为y=nx2-mx+m,
∵△ABC的派生函数与x轴有公共点,
∴△≥0,
∴m2-4mn≥0,
∵m>0,
∴m≥4n,
∵AB=AC,AH⊥BC,
∴BH=HC=$\frac{1}{2}$n,
∴cosC=$\frac{HC}{AC}$=$\frac{\frac{1}{2}n}{m}$=$\frac{n}{2m}$,
当m=4n时,cosC=$\frac{1}{8}$,
∴0<cosC≤$\frac{1}{8}$.
③如图3中,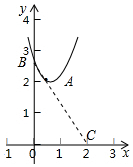
∵∠A=60°,AB=AC,
∴△ABC是等边三角形,设边长为a,
∴△ABC的派生函数C1为y=ax2-ax+a,
∴点B(0,a),顶点A($\frac{1}{2}$,$\frac{3}{4}$a),
∴直线AB的解析式为y=-$\frac{1}{2}$ax+a,
∴点C(2,0),
∴OB=a,OC=2,BC=$\sqrt{4+{a}^{2}}$,
a、当0<a≤2时,△BOC的派生函数C2为y=ax2-$\sqrt{{a}^{2}+4}$x+2,
易知函数C1与C2恰有一个公共点,请直接写出a的取值范围,
b、当a>2时,△BOC的派生函数C2为y=2x2-$\sqrt{{a}^{2}+4}$x-a,
易知函数C1与C2有两个交点,不符合题意,
∴当C1与C2恰有一个公共点时a的取值范围:0<a≤2.
故答案为0<a≤2.
点评 本题考查二次函数综合题、一次函数的性质、等腰三角形的性质、等边三角形的性质、派生函数的定义,解题的关键是理解题意,学会利用参数解决问题,灵活运用根的判别式解决问题,属于中考压轴题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 4.233×109 | B. | 4.233×1010 | C. | 4.233×1011 | D. | 4.233×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
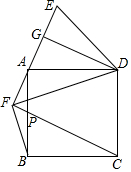 如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.
如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
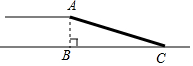 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
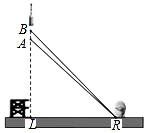 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com