
【题目】操作:将一把三角尺放在如图①的正方形![]() 中,使它的直角顶点
中,使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() ,探究:
,探究:
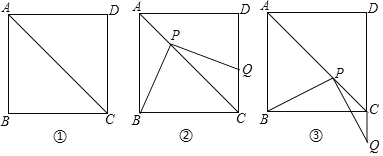
(1)如图②,当点![]() 在
在![]() 上时,求证:
上时,求证:![]() .
.
(2)如图③,当点![]() 在
在![]() 延长线上时,①中的结论还成立吗?简要说明理由.
延长线上时,①中的结论还成立吗?简要说明理由.
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)过点P作MN//BC,可以证明△PMQ≌△BNP,从而得出BP=QP;
(2)过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]() ,可以证明△PMQ≌△BNP,从而得出BP=QP;
,可以证明△PMQ≌△BNP,从而得出BP=QP;
(1)证明:过点![]() 作
作![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,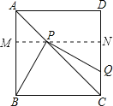
则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰直角三角形.
∴NP=NC=MB
∵∠BPQ=90°
∴∠QPN+∠BPM=90°,而∠BPM+∠PBM=90° ,
∴∠QPN=∠PBM,又∠QNP=∠PMB=90°,
在△QNP和△BMP中,
∠QNP=∠PMB,MB=NP,∠QPN=∠PBM
∴△QNP≌△PMB(ASA),
∴PQ=BP.
(2)成立.
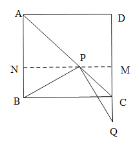
过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]()
在正方形![]() 中
中![]() ,
,![]()
∴![]()
∴![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中,
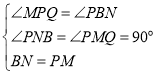 ,
,
∴![]() ,
,
∴![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
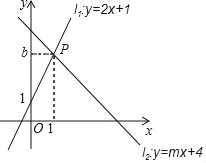
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现在剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的的高为_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从A地出发去25km远的B地,甲骑车,乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好为3h.
(1)若设乙的速度为x km/h,则甲的速度为 km/h,甲遇见乙时,乙走的路程可以表示为 km,甲走的路程可以表示为 km.
(2)两人的速度分别是多少?(请用方程来解决问题)
查看答案和解析>>
科目:初中数学 来源: 题型:
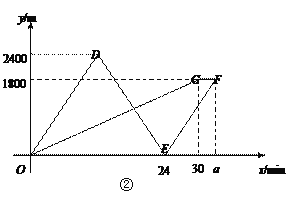
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2cm,AC=5cm,SABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
(1)在运动过程中,四边形AECF的形状是____;
(2)t=____时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com