
满足下列条件的各对三角形中相似的两个三角形有( ).
A、∠A=60°,AB=5cm,AC=10cm;∠A′=60°,A′B′=3cm,A′C′=10cm
B、∠A=45°,AB=4cm,BC=6cm;∠D=45°,DE=2cm,DF=3cm
C、∠C=∠E=30°,AB=8cm,BC=4cm;DF=6cm,FE=3cm
D、∠A=∠A′,且AB·A′B′=AC·A′B′
B
【解析】本题考查了相似三角形的判定
观察本题,发现每一选项中,都有一对角相等,都有两组边的关系式,可以利用两边对应成比例且夹角相等的两三角形相似进行判定.
解:A、∵∠A=60°,AB=5cm,AC=10cm;∠A′=60°,A′B′=3cm,A′C′=10cm,
∴∠A=∠A′,AB/ A′B′=5/3,AC/ A′C′=1
∴AB/ A′B′≠AC/ A′C′,
∴△ABC和△A′B′C′不相似;
B、∵∠A=45°,AB=4cm,BC=6cm;∠D=45°,DE=2cm,DF=3cm,
∴∠A=∠D,AB/ DE= BC/ DF=2
∴△ABC∽△DEF;
C、∵∠C=∠E=30°,AB=8cm,BC=4cm;DF=6cm,FE=3cm,
∴AB/ DF= BC/ FE=4/3,
又∵∠C∠E不是夹角,
∴△ABC△DFE不相似;
D、∵∠A=∠A′,且AB•A′B′=AC•A′B′,
∴AB=AC,
∴△ABC和△A′B′C′不相似.
故选B.


科目:初中数学 来源: 题型:
| 960 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
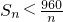 ;
;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 960 |
| n |
查看答案和解析>>
科目:初中数学 来源:2005年浙江省温州中学自主招生考试数学试卷(解析版) 题型:解答题
 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com