
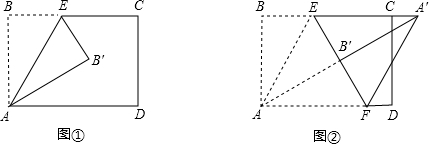
| A. | 只有②正确 | B. | 只有①②正确 | C. | 只有①③正确 | D. | ①②③都正确 |
分析 ①正确.只要证明∠AEF=∠EAF=∠EFA=60°,即可推出△AEF是等边三角形.
②正确.只要证明四边形AEA′F是菱形即可.
③错误.AB、BC的长度不确定,无法判断AC与DF的大小关系.
解答 解:∵∠BEA=∠AEF=∠A′EF,又∠BEA+∠AEF+∠A′EF=180°,
∴∠BEA=∠AEF=∠A′EF=60°,
∵BC∥AD,
∴∠BEA=∠EAF=60°,
∴∠AEF=∠EAF=∠EFA=60°,
∴△AEF是等边三角形,故①正确,
∴△EFA′是等边三角形,
∴AE=EA′=A′F=AF,
∴四边形AEA′F是菱形,
∴EF垂直平分AA′,故②正确,
由于AB、BC的长度不确定,所以AC不一定等于DF,故③错误,
故选B.
点评 本题考查翻折变换、线段的垂直平分线的性质、等边三角形的判定和性质、矩形的性质、菱形的判定和性质等知识,解题的关键是灵活运用所学知识,属于基础题,中考常考题型.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
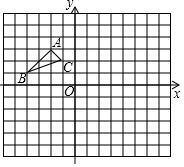 如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).
如图所示,△ABC的顶点分别为A(-2,3),B(-4,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2<m<-$\frac{2}{3}$ | B. | m>-2 | C. | -2≤m≤-$\frac{2}{3}$ | D. | m<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (8-6)÷8 | B. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{6}$ | C. | $\frac{1}{6}$÷$\frac{1}{8}$ | D. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com